Vibration »

Question: Why are vibrations so important to us?

Answer: Vibrations are phenomena of repetition, circular movements, and each transformation is a rotation (Space-Time, 1.4.2 Rotations). Rotations are all kinds of quantum evolution, and then all quantum states (due to the state-process dualism). Theoretical physics too often, almost constantly underestimates vibrations, unlike, say, the technology.

We know what a breakthrough in the application of electricity Nikola Tesla (1856-1943) made by alternating currents and rotating magnetic fields. Add to this how unimaginable electric and magnetic charges are without waves and the notion of matter in general (Quantum Mechanics, Louis de Broglie, 1924).

In addition to the classical treatment, the (hypo) thesis is possible that the electrons at rest are actually "attracted", but as soon as they move relative to each other to repel (Current), and then the transfer of a virtual photon between electrons (Multiplicities, Feynman diagram) acquired an associated meaning.

Vibration with such a continuation becomes what generates Coulomb force, so dramatic, though, that we still hardly notice the gravitational, or similar effects of the substance (Forces). Those who are consistent with the mentioned observation should not be surprised by the "antigravity" phenomena of vibration of the substance.

Here are just a few of the "countless" examples. I often repeat that every flicker carries some information and every detection goes with some oscillation (Frequency). This requires the survival of this world, which would not exist without "locking in periodic phenomena" (Chasing tail), because all of us together would be quickly consumed by the principle of least information.

Radiation »

Question: Can you explain Hawking radiation to me?

Answer: The radius of the black hole, which was first calculated by Schwarzschild from Einstein's equations (1916), was included in the previously known Stefan-Boltzmann law of black body radiation (around 1880). That calculus is a simple mathematics of simple fractions. We get a positive black hole temperature, which tells us that it radiates, evaporates and wears out slightly. Hawking (1973) added an explanation using microphysics (Hawking radiation).

Question: Does this agree with information theory?

Answer: Yes, that Hawking and information theory agree well. According to (my) information theory, the entropy is lower in the gravitational field than outside and, consistently, any gravity has a higher temperature.

Question: Where did the ideas about the entropy of gravity come from?

Answer: Gravity attracts bodies and accumulates information, and with greater information comes less entropy. This contradicts the common opinion of even the founders of the classical theory of information (Gibbs 1873, Shannon 1948), that entropy and information are one and the same phenomenon, or at least growing together. They are often marked with the same letter, but physics is not very consistent in that and its terrain is still Terra incognita.

In the same direction (with increasing entropy, gravity and information) there were more and lesser-known theories today, for now unrecognized. That bodies spontaneously move towards greater entropy, seemingly consistent with the Second Law of Thermodynamics, and that they fall that way, was somehow "logical" at the beginning of the 20th century. In the time of the Nazis, this (hypo) thesis became very popular, that the Sun and the stars are pieces of ice (Icy Sun), probably as an opposition to "Jewish physics", primarily Einstein.

Question: Aren't these reasons in contradiction, that gravity is an attractive force and that it accumulates information, with the consequences you state?

Answer: Not if gravity is not a force, but it works the way Einstein suggested. Movements instead of due to force, are a consequence of the curvature of space-time events (given places in moments) along shorter paths, i.e. geometry. If something really pulled the body towards the source of the gravitational field, it would deviate from its path (parabola, hyperbola, ellipse) and go directly to the center. But that's not all, the state of contradiction is not "approximately" a situation.

Anomaly »

Question: Is the sound antigravity?

Answer: "Sound is almost like antigravity," said Ira Rothstein at Carnegie Mellon University in Pennsylvania (Sound waves), because it has a negative mass and floats up, up and further all around us - albeit very slowly.

An anomaly is something that deviates from what is standard, normal or expected, and the behavior of sound in a gravitational field belongs to that type. The same can be said for the geyser, because all the liquids fall, go down to the ground, and they go up as if they are antigravity. In relation to the principle of the least action of physics and storms also are anomalies, restlessness despite spontaneous inaction.

The Gibbs Paradox (Action of Information) can also be considered a kind of anomaly. Gibbs (1875) imagined a vessel of "indistinguishable" gas particles (like the bosons we know today) that can be divided into two by a partition. By removing and then returning the barrier, the entropy of the vessel seems to first increase and then decrease, contrary to the Second Law of Thermodynamics and the spontaneous growth of entropy.

There are various (good) known solutions to Gibbs' paradox, and I just remind you that I add one more to the theory of information, about the remark that the "law of spontaneous growth of entropy" does not apply to space (bosons). At the same time, the entropy of the substance (fermion) of the universe increases, while its information decreases, in favor of growing space from which more and more extensive memories act on the current present — keeping the total information of the present constant (Growing).

An anomaly of the principle of minimalism of information in society (Equality) would be the need for equality (Why Equality). By equalizing the chances of information options, the system grows — contrary to the natural tendency to reduce information, onto inaction. Similarly, the natural tendency towards multiplicity, what that we can interpret the "objectivity of uncertainty", as if it opposes the more frequent occurrence of more probable outcomes, i.e. the principle of minimalism of communication (interaction).

A kind of anomaly of principle multiplicity would be the uniform repetition of the oscillation of a photon (light) isolated from its wider environment. However, the mentioned anomalies are not true disputes of some general regularity, but in the worst case its clarification, because otherwise, in exact science, we would not talk about an alleged anomaly, but about rejecting the law.

Forces »

Question: I am interested in the observation about electromagnetism (Current), it is very unusual. Do you have anything similar about gravity?

Answer: Yes, if you’re aiming for the difference in the positive charge potential of the nucleus of an atom and the cloud of negative electrons around, I’ve dealt with that. I like the elegance of that idea, the gravity by the electromagnetic force, but not its (banal) simplicity that bypasses multiplicity, otherwise a more important feature of the "information universe".

The idea of the difference between the potentials of negative and positive charges of an atom, due to the circulation of electrons around a proton and the inequality of their distance to another atom or point on a substance, while using the above observation of attracting currents in the same direction, can be adjusted in 2.27 × 10³⁹ times weaker gravitational force. Such an extremely weak attraction, supposedly gravitational in that contemplation, will not have a significant effect on the "currents" of the substance and there will be no repulsion (as with the electrons themselves).

The recent measurement of gravitational waves and perhaps the confirmation of the existence of subtle gravitons, their quantum spin ± 2, also supports this. Such gravity is not a micro but a macro phenomenon. Namely, the spin of the fermion (elementary particle of the substance) is ± ½ and it is not possible to add it with ± 2 and get some of the two, and the total spin before and after the interaction conserved. Therefore, speculation about gravity, due to the difference between the potentials of electrons and protons of atoms, should not be rejected too quickly.

However, on pages 74-78 you will find something much better in my book "Minimalism of Information". It is a derivation of Einstein's general equations of relativity from the principle of least action. The principle that has been tested in all cases of physical movements known today, and is part of the principle of least communication (my) information theory.

Equally correct different interpretations that lead to the same results are the characteristics of mathematics, so I do not run away from such in information theory. According, don't be confused by the following versions of gravitation theories.

Gravitational waves propagate on a spherical surface that increases with the square of the radius. We can assume that their specific energy, surface units, weaken to the same extent, and that they thus define the geometry of space (Space-Time, gravity) and its Gaussian curve (Inflexion).

Information theory also adds new meaning to this. As spherical waves originate from the same center, they will be "simultaneous" (Conservation) and in quantum entanglement (phantom action at a distance). The total action of a sphere and the wavelength can be constant over time but the amplitudes and its chances of interaction decrease with the surface — as well as the gravitational force.

It is a description of gravitational force in the manner of Feynman diagrams adding the information as "spice". The law of conservation (as for energy) also applies to it, but it is two-dimensional (Dimensions). A variation on this theme is the gravitational force from Kepler's second law (Notes I, Central Movement I and II), or vice versa, Kepler's law from generally constant central forces. Both of these cases are easily transferable to interpretations of electromagnetism.

All these descriptions are accompanied by more frequent occurrences of more probable outcomes or the less frequently informative ones. The principled minimalism of communication (interaction) speaks of the tendency of physical systems towards non-action (inertia), but also of the effort of the accumulated information (mass) to somehow dilute. Look for details in my earlier texts.

In the gravitational field, a part of the substance goes into parallel reality in relation to the relative observer. For such, the events of the own (proper) observer are reduced. Therefore, the relative passage of time is slower, and hence again the "gravitational attraction" of the space of slowed down the time, that is, the principled information repulsion of accelerated time.

Question: Is antigravity possible?

Answer: Yes, just as a theoretical possibility. That is the level of loose hypotheses, that physical bodies are gravitationally repelled. The first, which is not originally mine, I discussed in the book "Quantum Mechanics" (1.4.1 Time inversion, Charge inversion). It sees in the symmetry "charge-parity-time" (CPT symmetry) the possibility of gravitational repulsion between matter and antimatter. I don't take it seriously.

The second, which is originally mine, I did not decide to mention in that book, and it concerns the electric current (Current) and the above speculation about the different Coulomb force at a point outside the atom, given the different distances of electrons and protons from that point. It is a concept according to which charges of the same name are repelled in mutual movement (approaching or moving away), and otherwise they are "attracted".

The attractive gravitational force, created in this way, would arise from different distances of a given point outside the atom to the clouds of electrons and protons of the nucleus and thus caused potential differences between electrons and protons. It is possible to statistically estimate it to be about 10³⁹ times smaller than Coulomb, which is a well-known relationship between these two forces (electromagnetic and gravitational).

Note that these are not the only ideas about negation of gravity (Anti-gravity). Also, that the accuracy of the initial (hypo) theses, on CPT symmetry and potential difference, does not guarantee antigravity as a consequence, but also vice versa, that the possibility of electrostatic levitation (Hovering Rover) does not imply the electromagnetic nature of gravity.

Symmetry »

Question: This view of electromagnetism (Current) is becoming more and more interesting to me. Do you have anything else you could (want to) say?

Answer: Yes, I will tell you something else, if you accept that as a kind of very rough, rude speculation that I keep in stock, knowing that I will be able to erase it with other mistakes by testing.

First of all, know that "symmetry" means the property of immutability in certain changes. Thus, "translation", such as preserving the contents of a wagon as it moves on rails, maintains the reciprocity of all given points, but not them in relation to an environment. It can be reduced to two central symmetries, and each of them to rotation in the same plane by an angle of 180°. Rotation for the same angle through some external dimension will give each of the reflections (axial, mirror) and, in general, all the symmetries of a rotation. This is dictated by mathematics to the exact sciences.

Let's move on to physical forces. Although there may seem to be many more, there are only four fundamental forces of nature: gravitational, electro-magnetic, strong and weak nuclear. Let's say that in the previous (Forces) I hit the description of gravity with electromagnetism, so let's move on to a strong nuclear and weak force.

The force that can hold the nucleus together against the huge proton repulsion forces is really strong (The Strong Force). However, it is not an inverse square force like the electromagnetic one and its range is very short. That range, 10^-15 m, is the diameter of the nucleus of an atom of medium size, which means that what a strong force acts on literally rests on the nucleus. Protons (positively charged) have nowhere to go when they are pulled by the "attractive force of the same name" (Current) and in that concept it is just such a good candidate for "strong force".

We consider a strong nuclear force, which is also called a strong nuclear interaction, to be the strongest of the four fundamental forces of nature. It holds together the quarks that make up protons and neutrons, and part of the strong force also binds the protons and neutrons of the atom's nucleus. However, it is about 10³⁹ times stronger than gravity, which is a number that gives importance to the previous "guess" about forces. It reinforces the idea that this force and gravitational force can be electromagnetic in nature.

A weak force, also called a weak nuclear interaction, is responsible for the decay of particles, which is a literal change of one type of subatomic particle into another (The Weak Force). Thus, for example, a neutrino that strays near a neutron can convert a neutron into a proton while the neutrino becomes an electron. This interaction occurs by the exchange of W and Z particles, the boson mediator. When subatomic particles such as protons, neutrons and electrons are found at a distance of 10^-18 meters, or 0.1 percent of the diameter of the protons, from each other, they can exchange the mentioned bosons.

This distance is just enough for the described repulsion of the charges of the same name to occur, or here, gravitational attraction due to the (statistical) difference in the distance between the outer electrons and the inner protons of the substance's atoms. In official physics, from the unification of weak and electromagnetic into one electroweak force (1979) and measurements of W and Z particles (1983), it is believed that at very high temperatures and energies over 100 GeV these particles become identical, and weak and electromagnetic interactions then the manifestations of one force.

In the 1970s, Sheldon Glashow and Howard Georgi proposed the Grand Unification of strong, weak and electromagnetic forces at energies above 10¹⁴ GeV. For such a high average particle energy, if the current interpretation of thermal energy is valid, a temperature of 10²⁷ K would be required. As temperatures in the stars range from 2,500 to 50,000 Kelvin, the aforementioned "great unification" may be left with only the early stages of the universe's formation.

It is clear that these "unifications", even if they seem unfinished for now, support my above explanations. They also support the (hypo) thesis on the constant creation of the universe (Growing), which increases entropy by cooling, decreases substance information and increases order (number or density of natural laws), so they are in line with information theory.

Question: I find these interesting, you say speculations, and why did you start the story with symmetries?

Answer: Weak and electromagnetic forces look very different in the current universe with relatively low temperatures. But when it was much warmer, balanced thermal energy of the order of 100 GeV, these forces may have been essentially identical — part of the same unified "electroweak" force. With masses around 80 and 90 GeV, respectively, W and Z were the most massive particles seen at the time of discovery, while the photon was massless. The difference in mass is attributed to a spontaneous violation of symmetry as the hot universe cooled.

The symmetry was spontaneously broken when the available energy dropped below about 80 GeV and weak and electromagnetic forces took on a distinctly different appearance. The model says that at an even higher temperature, symmetry or unification occurs with a strong interaction, the aforementioned large unification. And even more, that the force of gravity can join them so that the four fundamental forces prove to be one single force.

The basis of this recognized theory is the concept of spontaneous symmetry breaking, without which there is no electroweak unification and further unification. Hence, the package also includes some examples, analogies in the field of classical physics.

For example, snowflakes. Hydrogen and oxygen molecules are quite symmetrical when isolated. The electric force that controls their actions as atoms is also the force that acts symmetrically. But when their temperature drops and they form a water molecule, the symmetry of the individual atoms is broken as they form a 105-degree molecule between the hydrogen-oxygen bonds. When they freeze and form flakes, they form a different kind of symmetry, but the symmetry of the original atoms is lost. Since this loss of symmetry occurs without any external intervention, we say that there was a spontaneous violation of symmetry.

I add to this that all quantum states and processes (which are dual vector-operator phenomena) are otherwise represented by some rotations, i.e. symmetries, and they are, again, forms of "Information Perceptions".

137 »

Question: You believe in the multiplicity of information and you hope for a unique theory of forces, isn't that a bit controversial?

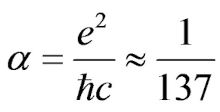
Answer: These "four fundamental forces" are small in relation to the "multiplicity" of nature, they only seem big to us little ones.

However, a kind of unique theory of physical forces already exists in the theory of "potential energies". The lower potential energy is attractive and the higher is repulsive, and this applies not only to all known forces (derived from fundamental ones), but also to those that are yet to be discovered (A New Force).

If information is equivalent to action, which is a product of energy and elapsed time, it will be that in constant time intervals the principle of least information becomes equivalent, equal to the theory of potential energies. Both are expressions of spontaneous, more frequent realization of more probable outcomes.

The information is transmitted in the smallest packets, which is why the action is quantized (ΔE Δt ≈ h). At equal intervals of time (Δt = const.) the energy is atomized (Greek: atomos — indivisible), so is the velocity of the electron in the first orbit of the atom (v = αc). This was the idea of Sommerfeld (1915) when he discovered the fine structure constant (α = 1/137) which then became the obsession of many physicists (the number 137).

Physics quickly discovered that the various relationships between the elemental charge (e = 1.602 × 10^-19 C), the speed of light in vacuum (c = 300,000 km/s), Planck's constants (h = 6.626 × 10^-34 J⋅s), i.e. reduced Planck constants (ℏ = h/2π), and vacuum dielectric constants (ε₀ = 8.854 F⋅m^-1) are in relations to the Sommerfeld constant (Fine-structure constant).

A strong connection, the relationship between the listed quantities would be really very strange if we thought that the phenomena that define them do not come from the same source. I hope that these coincidences become clearer to us now with the knowledge of the breadth of the "principle of information minimalism". This is also the answer to the above question.

Packages »

Question: Why are our perceptions always in the final packages?

Answer: I don't know why they are exactly as they are, in final portions, but because they are, we have the laws of conservation, not only information, but also physics. From infinite sets, it is possible to infinitely separate finite and even infinite subsets, so that the main set always remain the same.

Legal regulations, mathematical claims and steps of proving theorems, the action of the microworld, or the uncertainty of duration as well as energy from the point of view of each individual observer, are always discrete quantities. The consequences are our final perception in the sea is something infinite, which is impossible to fully perceive.

The weaving of space, time and matter is information, the magnitude of which comes from uncertainty. No matter how big package, or packages of it you comprehend, it is always some information that in itself, but also for others, has a dose of unpredictability. Therefore, there is no set of all sets (Bertrand Russell, 1901) nor is there a theory of all theories (Kurt Gödel, 1931).

We are talking about quantities, about information that can be less and less, but not further than some of the smallest packages of pure uncertainty. To subtract something from such an atom (Greek: ἄτομον — indivisible), a quantum of information, means to reduce its uncertainty, that is, to gain certainty. In that sense, the smallest packets of information are optimums, local extremes in the language of infinitesimal calculus.

Somewhere in the meantime, on the scale of the size of this side world (macro world), the processes of uncertainty can be locked in circular flows (Cycles). As unpredictability is the deepest structure of space, time and matter, so that repeated "news" is no longer news, with the law of conservation, information inevitably leads to cyclical "development" (Chasing tail). Thus, the dual particle-wave nature of matter, in information theory, becomes a question of the survival of the universe.

Rank »

Question: What is the rank of a linear operator?

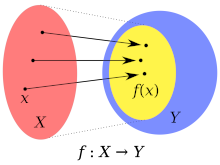
Answer: The figure on the left shows the mapping (of the elements) of the set X into Y by the function f. A function is a special type of relation, connecting pairs (x,y), elements of the first with elements of the second set, considering their order. In the set of pairs, the elements of the first set can appear only once.

Elements from X are originals, and those from Y are copies. From the first are the items from the second its images, or we say that X is a domain and Y is a codomain. We also call Y the area of function definition, or range. The function is linear when the growth of the value of the domain elements follows the proportional growth of the codomains. For example, when f duplicates twice the original, the copy is doubled too.

A special type of these are linear operators that translate series of values (vectors) of domains into series of values of codomains. This gives a new quality to the use of functions. For example, in two groups we have x₁ and x₂ people. We will give each of the people from the first (second) group a₁ (a₂) pieces of pastry and b₁ (b₂) pieces of cake. Then:

where y₁ is the number of total pieces of pastry, and y₂ is the total number of pieces of cake. Behind this idea of linear operators is a lot of mathematics, linear algebra, so that in the end the same system of linear equations can be written simply and elegantly:

In the above example, for two (one) person of the first (second) group, with a total of ten and five pieces of pastries and cakes, we calculate that the division must be three (four) pieces of pastries and two (one) cakes. Check it out!

We work similarly in quantum mechanics, where the coefficients of this matrix M, the first row (a₁, a₂) and the second row (b₁, b₂), can be complex numbers, and the components of the first vector X = (x₁, x₂) can also be complex, as of the second Y = (y₁, y₂). We can work comfortably with the operator matrix, because one theorem says that they are "isomorphic", that there is a two-way unambiguous association (bijection) between the operator and the corresponding matrix, and they are equivalent.

When the matrix of the second order maps each vector with two components into a two-component vector, we say that it is "regular". In general, a vector with a natural number of n components is mapped by some n-order regular matrix (n rows and n columns) to some n-components.

Because regular operators (matrices) map n-dimensional vector space into n-dim, we no longer call the rank of such by the details of an infinite set of points of their spaces, but simply consider them as their dimension. The specified system, i.e. its matrix has a rank of two and the same number of dimensions (which should be distinguished from the dimension of physical space-time). All equally dimensional vector spaces are isomorphic.

The magic of this algebraic story does not end here. Operators and even matrices are also types of vectors. Moreover, they are "dual" to the vectors they act on, forming two equivalent types of space between which there is a mutually unambiguous mapping, but we avoid calling them isomorphic when emphasizing differences in the measurement of their intensities (metrics).

We know that quantum states and quantum processes are representations of vectors and operators (Hilbert spaces). But, according to these "miracles" of mathematics, they formally behave in the same way, so everything that can be learned from quantum algebra about the behavior of particles will apply equally to their changes. The incredible consistency and accuracy of algebra in the interpretation of quantum measurements still confuses us, but even more than that, some intuitive, physical descriptions of events confuse us, occasionally to the point of complete misunderstanding.

I clarify some of these obscurity with information theory. The fact that quantum processes are made only by regular operators tells us that they are all reversible, to remember where they came from. In addition, they are also "unitary", which means that they are of unit intensity, i.e. they do not change the intensity of the vector they change, which tells us that the laws of conservation apply to all these processes. I added "only", and that is an important detail, that they all talk about information.

Everything that can be perceived is somehow perceived — is the consequence of the state-process duality, and the consequence of the equivalence of space of equal dimensions — that perception is everything in the world of physics.

Information »

Question: Explain to me briefly the concept of information?

Answer: Information is a measure of the amount of options. The options can be 8 when you need to imagine one of the numbers 1-8 which I then guess with binary questions ("Does ...?"). The number of answers (yes-no) is information, which in that case is 3. Such its (equally probable options) basic form is logarithm.

Another example of this, information of equal opportunity, or Hartley's (named after the engineer who first defined it in 1928), is the search using scales (Physical Information).

When we are looking for one that is damaged among the eight equal weights and is a little lighter than the others, we first divide them into two groups of four, put each on one of the two bowls and separate the lighter group. Let's divide the lighter again into two groups of two and single out the lighter one. In the third step, we divide the lighter into two groups of two weights and separate the lighter ones. This is damaged and separated in three measurements, which means that the information h = 3 possibilities x = 8.

In general, in binary searches, for x = 2^h possibilities the information is h, or what is the same, the information h = log₂ x is a measure of x possibilities. It is in binary digits (bit). Information (h) is the quantity, the number of binary digits required to write x equal possible values. In the decimal system of numbers, we would work analogously and have the information of the logarithm base ten (h = log x), and the unit "decit". In the base of e ≈ 2.71828, the natural logarithm (h = ln x), the unit of information is "nat" (natural).

When we have the distribution of probabilities, through the outcomes of probabilities p_j, indexes j = 1, 2, ..., n, of which one and only one can happen, individual information will be h_j = ln p_j nat. Then the mean value of all of these is s = Σ p_jh_j, where it is added to all indices, and that is Shannon's (1948) definition of information.

The law of conservation does not apply to Shannon's information, so in the above-mentioned book I found the most similar forms to which that law would apply. But let's not complicate things now, let's stick to Hartley's definition that conserves quantity. Namely, if 2³ options can be made with 3 binary digits, and 2⁴ outcomes with 4, then with 3 + 4 = 7 digits we can combine 2³ ⋅ 2⁴ = 2^{3 + 4} = 2⁷ possibilities. That is, ln 2³ + ln 2⁴ = ln 2⁷, because it is precisely the logarithm such additive function, as created for physical information, for which the law of conservation applies.

Just as physics treats reality with real numbers from its equations, information theory that recognizes the objectivity of chance will treat pseudo-reality with imaginary and complex numbers. Then Hartley's information is defined by Z = e^H, ie H = ln Z, where "information" H and "number of options" Z are complex numbers.

We immediately see that the "physics" of information theory works with periodic phenomena, because we know that the exponents and logarithms of complex numbers are periodic. In fact, it is more real than real physics, due to the wave nature of matter in general. With this, we have already gone beyond the required brief explanation of the information, and below it is up to you to read perhaps my light contribution on Quantum calculus, or some of the current work on such a computer (Quantum Information).

Oscillation »

Question: Do you have any example information other than these classics?

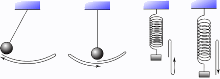
Answer: I have enough of them, of course, and the oscillations are just the most interesting for my information theory (Vibration), so here is one of them unknown.

In the picture on the left we see one full oscillation of the pendulum and the spring. A similar thing happens with "pure" information, where it should be noted that its smallest free, moving quantity is contained in one quantum (h ≈ 6,626 × 10^-34 m²kg/s — Planck's constant).

This smallest load-bearing package is, for example, the product of changes in energy (ΔE) and elapsed time (Δt). Then we talk about the "quantum of energy" (ΔE ⋅ Δt = h). But the quantum is also the product of changes of the momentum along the abscissa (x-axis) and the abscissa itself, the "quantum momentum" (Δp ⋅ Δx = h). As changes are inevitable, because repeated "news" is not news, so are the traps for information (Chasing tail), due to the law of conservation.

Assume that in the first step, regardless of the change of time or path, we have the corresponding changes from a₁ = a + b to b₁ = a - b, either energy or momentum of the quantum, where a and b are some predetermined constants. The change is repeated, so in the second step we have a₂ = a₁ + b₁ = 2a and b₂ = a₁ - b₁ = 2b. It will be in the third and next steps:

We see that in the general, nth step we need to distinguish the even n = 2k from the odd n = 2k + 1 numbers, respectively for k = 0, 1, 2, ..., where a₀ = a and b₀ = b, and the following proof is the method of mathematical induction which here is quite simple.

For the first step of induction, the first two-step is sufficient, for k = 0 and k = 1, and then the general formulas are obviously correct. Assuming that the general formulas given are correct and deriving the following is the second step of induction:

From the assumption that the formulas in the nth step are correct, we derived that they are also true in n+1. This completes the proof by induction.

By substituting the energy and time in these formulas, i.e. the momentum and the path, the intermediate steps k become information, and the numbers x = 2^k the amount of options similar to those from the previous examples (Information). Again, k = log₂ x, so you have the example you were looking for.

An interpretation consistent with (my) information theory would be as follows. At every moment of the present, there is exactly one step from the mentioned "oscillations", in order, and from that point of view, respect for the law of conservation information. However, they remain in the past, from which they also act on the current present, weakening as they get older, so their additional effect should be compensated with something — for the sake of the law of conservation information in wider parts of the universe.

Information theory offers such compensation. It occurs with a very slow, statistical, but persistent and spontaneous increase in the entropy of the substance, which "melts" the information of the substance of the universe into space and expands space.

Space is created exactly at the speed at which the information of the substance disappears. At the same time, it is possible that parts of space disappearing, going beyond the "event horizon", beyond the borders of the universe visible to us, so I expect a balance of these processes. Well, that as much information reaches the present from the past as it disappears out of the present itself.

Conjecture 2 »

Question: What is the point of the "new" oscillation model?

Answer: You have already stated that (Oscillation). That the example demonstrates the trapping (Chasing tail) oscillations and the analogy of the movement of particles-waves, say photons, while consistently following the theory of information.

When we throw out that moment of the mentioned example, the trap of oscillations, we could try to understand the rest by tossing a coin successively. In the first throw (n = 1) the possible outcomes are {H, T}. After two throws, the history of possibilities is {HH, HT, TH, TT}, and after n = 1, 2, 3, ... there were 2ⁿ possibilities. Namely, in each next step, each of the previous outcomes H (head) and T (tail) is doubled.

We imagine that our reality has somehow developed in this way. Let’s add a geometry to this conjecture (opinion based on incomplete information) in order to avoid the increase of errors and further stagnation, and in addition to the fact that its possible contradiction could be pointed out.

So, one of our present, 3-D spaces (without time), is just one of the points of the imagined also 3-D space of some abstract geometry. From the equivalence of moving our point with the development of this present, that is, with the course of real time, it is possible to draw many conclusions about the nature of this supra-geometry. To begin with, let us note that it fits well with earlier stories about the six dimensions of space-time (Dimensions).

Our "point" will move "by inertia" through its abstract space, if we harmonize its metrics (definition of distance) with the cause-and-effect processes of our present. For now, I leave aside the questions of "whether and why" that is possible. I emphasize the current conclusion, then, that the law of inertia also applies to the over-space, and then further that we can reach the principled minimalism of information in it.

An interesting idea is that the principle of least action, otherwise known to theoretical physics, together with its informatic extension to "spontaneously more frequent realization of more probable events", could be extended to the 6-D universe. But, let us note, it is quite logical in this theory of information — where information is the basic tissue of space, time and matter, and uncertainty is its essence.

Accordingly, our present closes in 4-D space-time spontaneously fleeing from excess options. And that there is a continuum (𝔠) of these options, I wrote (Values) "calculating" the countable infinity ℵ₀ = log₂ 𝔠, which can now be added to the meaning of our world: it is information about the possibilities of the wider world. I also have as a recent answer (Continuum) that not all possibilities can be listed in an endless sequence of events.

The previous discussion of Conjectures concerns primarily the axioms of infinity, but also this issue. I think that dwelling on the details of these otherwise extensive topics from set theory would unnecessarily burden this text, so I omit them.

Metrics »

Question: What kinds of "intensity" are you talking about?

Answer: The remoteness, distance d(x,y) between any points x, y and z has long been defined in functional analysis by:

So, distance is a non-negative real number, zero if and only if (iff) it is the same point. The order is not important here, and for the distances between the three points, the "triangle inequality" is valid. Then we notice that with a given natural number n = 1, 2, 3, ..., a point in n-dim metric space is always an n-tuple of numbers. Examples are:

In real space (Rⁿ) we have d(x,y) = (Σ|ξ_j - η_j|²)^1/2, where it is summed for all indices j = 1, 2, ...,n. This is the default metric. However, it is a subset of metrics (Rⁿ_p) where the parameter applies 1 ≤ p < ∞, when and the above conditions for distance d(x,y) = (Σ|ξ_j - η_j|^p)^1/p. In the case of p --> ∞, this metric becomes boundary, the limes d(x,y) = max |ξ_j - η_j|, where the largest absolute difference of all indices is taken. They are easy to translate into complex ones.

I have listed only some of the more well-known metrics, which do not require a definition of continuity, and look for other examples yourself. The first three of the above conditions for these are obviously met, and the fourth follows from Minkowski inequality:

where it is added to all indices j, and the parameter p ≥ 1.

The norm (intensity) of a vector (point) is defined by equality using metrics ∥x∥ = d(x,0). That the conditions of the norm were then met:

for all vectors x and y, and each scalar λ, it is easily proved. Otherwise, if a normed vector space is defined before the metric, the metric is defined by the norm with the equality d(x,y) = ∥x - y∥, which is also easy to check.

Another way to define the norm of a vector is by using the scalar (inner) product of the vector ∥x∥² = ⟨x, x⟩, for which:

for all vectors x, y and z, and each scalar λ. Cauchy-Schwartz inequality is so written |⟨x, y⟩|² ≤ ⟨x, x⟩ ⋅ ⟨y, y⟩.

For example, the Information Perception S = a₁b₁ + ... + a_nb_n is a scalar product of the vectors a = (a₁, ..., a_n) and b = (b₁, ..., b_n), which we write S = a ⋅ b, or S = ⟨a, b⟩. If the coefficients of these vectors are complex numbers of the form a = x + iy and the complex conjugate ā = x - iy, then S = ā₁b₁ + ... + ā_nb_n. Further generalization of the information of perception is possible (Quadratic form), and even necessary, but it will go with the definitions of norms that I did not state here.

Linearity »

Question: What is and how far does the "linearity" of functions reach?

Answer: The linear function f is defined by equality

The above definition can be divided into f(αx) = αf(x) homothety, and the additivity f(x + y) = f(x) + f(y), again where the constants α and the variables x and y are arbitrary. Such a function is (not) continue together with these values.

Note that the equation of the line "y = kx + n" in the plane (Oxy) is not a "linear" function, except when the line passes through the origin (O), with n = 0. In general, any "linear" function of the form is f(x) = λx for a constant λ, and in applications it is always approximate.

For example, the body moves uniformly with more time, crossing larger paths in the manner of linear functionality. Also, by selling more goods, the trader will earn more. But over time, the body encounters obstacles that disrupt the linearity of its movement, and a successful retailer may move to wholesale when profit percentages change.

The potential (E_p) and kinetic (E_k) energy of a body in free motion make its constant total energy (E = E_p + E_k). If we take the total energy for the zero level, the kinetic becomes proportional to the potential in the manner of a linear function (λ = -1). Furthermore, when at equal times we look at potentials as "field information", it turns out that the body seeks to (spontaneously) reduce potential energy, replace it with kinetic according to the principle of minimalism of information.

The linearity of the replacement of potential energy by kinetic will degenerate with the increase in the mass of the gravitational source, or with the entry of the body into very strong fields. Information theory then provides an interesting explanation that is consistent with the treatment of space-time dimensions and on the other hand with the principle of minimalism. The gravitational field, while losing entropy by attracting and accumulating information (substance), transfers parts of the information into a parallel reality — so that it constantly remains in its greater deficit the stronger the field.

Below is a seemingly completely different story. We know the duality vector-operator of linear algebra, hence the corresponding state-process of quantum mechanics. The forms of behavior of the body are equal to those of their changes, to the extent that we can write

The information of perception is also linear, for example its form S = S₁ + S₂, i.e. (a + b)x = ax + bx, previously mentioned more often (Components). This reduces it to linear algebra, and in such a way it is introduced into quantum mechanics. Together with Schrödinger's equation, in different ways, it is to be expected that the information thus defined will also be generalized by some new physicist. First, because of the limitation of linearity in the interpretation of the world.

Scattering »

Question: Does the Compton effect have anything to do with information theory?

Answer: I described this in detail in the book "Space-Time", from page 34, but it is easy to retell. The first part is the same as the one in Wikipedia.

Information theory considers (at least) two probabilities related to particle-wave. The first is about amplitudes, the well-known Born rule (same book, page 15), and the second is the probability of the trajectory that wavelengths tell us about. Greater blurring of a wave along the length of one oscillation reduces the probability density of its finding at a given place. This is new.

Uncertainties of particle-wave positions, according to information theory, are an expression of the probabilities of their trajectories. The Compton effect, which shows that the reflected (scattered) photon after a collision with an electron increases the wavelength (in the figure, λ < λ'), among other things (that this is proof of the photon particle structure, in addition to the wave), confirms this thesis.

Therefore, before the collision, the photon moves along a path of shorter wavelengths because it sees its path as more probable as such, and only when forced by an electron and collision will it turn to (from its point of view) a less probable path. Since the energy of the photon E = hf = hc/λ, where the constants h and c are respectively Planck's constant and speed of light, and the variables f = 1/τ and λ = c/f frequency and wavelength of light, the higher the wavelength corresponds to less energy. The information of light remains the same, because it is equal to the quantum of action which does not change (Eτ = h).

The principle of least action speaks of not changing the action unnecessarily, that is, of saving communication, and from this the probability. Alternatively, from the side of action and reaction or reciprocity (Gradient), we can see this as a decrease in photon energy by going to a "secondary" path (states of less probability), where the interaction of "ordinary" is less likely, when additional energies are needed to they dragged themselves into the "normal" world. Then, on the contrary, leaving "our" world with a part of the energy, the particles go "abroad". I paraphrase, of course.

Similarly, we can describe the redshift of the light of a moving source (ibid., p. 71). According to the theory of relativity, the observed transversal and mean longitudinal wavelengths of light are equal and increasing with the velocity of the source, proportional to the relative increase in energy of the system in which the light source is at rest. We can also understand this perception as a particle associated with the "foreign" (moving system) which has been deprived of energy from us (in relation to us) so that it such can be seen from the "domestic", the system in which we rest.

This is a bit of an unexpected view for official physics, but again it is less strange than some others, already routine for information theory. For example, when we say that the light of an outgoing source has a greater wavelength than its own (proper), and its own is greater than the wavelength of an incoming source, then we say that these lights trace the space-time of three conceptions. The past of the outgoing source, the present in which we rest and the future of the incoming source.

We consistently believe that the wavelengths of these worlds are a message to us about uncertainties, about the amount of our communication, in order from: past, present and future. That is how the present moves towards the future, and not towards the past, because they get less information from there. This is consistent with the principle of minimalism.

Majorana »

Question: What are "quasi-particles"?

Answer: By the way, in physics, "quasiparticles" and collective excitations (which are closely related) are phenomena of "emergence" that occur when a microscopically complicated system, such as solid matter, behaves as if it contains various particles with weak interaction in vacuum. Anyons are an example of such.

But I guess you also mean the particles that the Italian physicist Majorana theorized about in 1937, following Dirac's idea of antimatter (First sighting). He predicted that there were some particles among fermions, named after him, which did not differ from their antiparticles.

Mysteriously, the physicist disappeared during a ferry trip along the Italian coast only a year after he gave his prediction. Scientists have been searching for Majorana's enigmatic particle ever since. It has been suggested, but not proven, that a neutrino can be such. On the other hand, theorists have found that Majorana fermions can also exist in solids under special conditions.

As we know, quantum phenomena are representations of abstract linear (Hilbert) algebra. From habit, the classical physics, we divide the vectors of these spaces into states and processes, although they can be elements of equal, more precisely isomorphic or dual, vector spaces. They are sequences of (complex) numbers or matrices, as well as wave functions and their linear operators, i.e. mappings and mappings of the mappings.

A function that transforms a function, as well as a vector that changes a vector, or a number that represents the number of numbers, is a way of seeing the world using mathematical methods. The novelty now is that we do not have to formally distinguish a physical quantum state (a set of particles-waves) from a change of that state. The state evolves in a certain way and, dual, quantum evolution tends to choose the state. The amount of the very change is as constant as the amount of what is changed. Quite suitable for information theory.

Hilbert space operators are unitary, which means that they preserve the inner product, that their norm is one. We say that they are regular, that their matrix is inverse, that is, that they reflect the laws of conservations, so they are very physical. Copies remember the originals and, at least theoretically, inverse processes are possible, changes that would translate future states into past ones (CPT symmetry). In addition, in the subtitle "Unitary matrix", on page 116 of the book "Notes II", we see that each of them can be presented as a rotation.

If A is a unitary matrix, its determinant is one, |A| = 1. It represents a photon or electron, state or process and can always be written as a product, A = BC, again of unitary factors B and C. It is a composition, a cascading mapping of some state (x) over time (x --> Cx --> BCx = Ax), which also means the existence of quasi-different particles of the same starting particle.

In particular, we know that the wave function of an antiparticle is the conjugate wave function of a particle. Thus (Majorana fermion) is the creation operator γ_j^† of a fermion, say an electron, in the quantum state j, and its annihilation operator γ_j. Unlike Dirac's fermions, these operators are identical. Dirac's particle is different from its antiparticle, Majorana's particle is also its own antiparticle.

The fermion operator, further, can be represented as the sum of two Majorana operators, c_j = (γ_1,j + iγ_2,j)/2 and c_j^† = (γ_1,j - iγ_2,j)/2. Its operators of creation and annihilation do not change by conjugation (γ^† = γ), and the imaginary unit changes its sign (i^† = -i). They are quasi-particles, and as operators, because of what has been said, they are mutually anticommutative. By changing the order of multiplication (affecting), they change the sign of the result.

It is similarly detailed with Marjoram bosons. Recent research predicts the splitting of photons also into quasi-particles (Split Photons). “This is a major paradigm change of how we understand light in a way that was not believed to be possible,” said Lorenza Viola, the James Frank Family Professor of Physics at Dartmouth and senior researcher on the study. “Not only did we find a new physical entity, but it was one that nobody believed could exist.”

Consistent with my theory, all quantum states are some packets of information. I mean that, noting that we have "free" information that moves with quanta and at least one type of "non-free" that quanta are made of. Analogously, quasi-particles would suit the latter, but that would be just the beginning of a story unknown to us for now.

Fields »

Question: I am still interested in that representation of gravity by means of electromagnetism (Forces) and it is not at all clear to me why you persistently do not believe in this possibility?

Answer: Because gravitons are not the same as photons. So much to a careful one is enough. I am open to doubt, I repeat, and do not insist on negation.

Question: So why did you deal with it so much and do so many calculations?

Answer: Out of curiosity. It's for fun. Out of a desire sometimes not to deal only with the truths. Why do people read fairy tales.

Question: Does that mean you have another alternative idea, the theory of forces?

Answer: It's kind of like that. I understand it as a continuation of field theories using information theory, which was actually started by the genius Michael Faraday. I recommend to bestir by reading a light article about it (Heart of Physics) or listening to an interesting lecture (David Tong), not to be burdened with too many "known facts", and as an introduction to more serious work.

The idea of information is a simple addition. From certain centers, which can be called real particles-waves, 2-D virtual particles-waves spread spherically, which are therefore simultaneous on the surface of the current sphere (Dimensions), which means that the sphere is a quantum entanglement.

The beginning of the story is a combination of Einstein's "spooky action at a distance" (Conservation) and Feynman's diagrams (Quantum Mechanics, p. 37), but in the sequel, which I still need to work on, I believe I will find something from a wider repertoire of information (Multiplicities).

Gradient »

Question: Does the "field of information" behave consistently with the principle of minimalism?

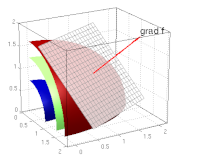
Answer: Yes, and consistent with that are the ongoing of action-reaction, or cause-effect, as in the fabulous dance of couples where the partner can be the more than one, and even in the game "Tit-for-tat". Let's look at the explanations respectively.

A gradient is an increase or decrease in the size of a property (temperature, pressure, density) when moving from one point or moment to another. In vector analysis, the gradient of the scalar field, f = f(x,y,z), is the vector field, grad f = ∇f = (∂_xf, ∂_yf, ∂_zf), which has the direction of the largest increase in the scalar field, i.e. whose intensity is the greatest change in the field (Space-Time, p. 35).

For example, the temperature of a part of space, which slowly changes from point to point and takes the values T = T(x,y,z), will have currents (flux) with the direction and intensity of the vector "grad T". The picture above on the left shows how this vector is (always) perpendicular to the "scalar field", now temperature values.

See the proof in the mentioned book, and the explanation is in the Second Law of Thermodynamics and the position on the increase of entropy with the decrease of information. Namely, heat (energy) goes from a body of higher temperature to a neighboring body lower, which the account sees as a spontaneous increase in entropy (heat and temperature quotient), due to which "wild" oscillations of molecules are reduced, and "amount of uncertainty" (information) cooled decreases.

I intentionally detail this about the increase in entropy that goes with the decrease of information, because in some circles in physics there is still a (in my opinion wrong) belief that higher entropy corresponds to higher information, not less. Then there is the principle of minimalism of information, according to which higher heat has higher radiation of information (and therefore energy) and the shortest way to the outside, which expresses the vector heat gradient (∇T).

It is similar with divergence (div v = ∇⋅v), which in vector analysis is a vector differential operator, which measures the intensity of the source or abyss of the vector field v at a certain point and results in a scalar field. When this field is electric, ∇⋅E = ρ/ε₀ is the first Maxwell's equation, where ρ is the charge density, and ε₀ = 8.854 × 10^-12 F/m is the dielectric constant of vacuum. For the magnetic field we have the second Maxwell's equation ∇⋅B = 0.

The increment of divergence (div v = ∂_xv_x + ∂_yv_y + ∂_zv_z) is the sum of three additions by components. Without change, there is no divergence, no gradient, and no information. Where there are different values by position, divergence expresses the flow of the field from the points of stronger places to the weaker ones. This is in accordance with the principle of least action (informatiton).

Finally, the rotor of the vector field, rot v = curl v = ∇ × v ("∇ ×" pronounced "del cross"), is a vector that in vortex fields is an expression of the circulation of the vector field through the contour surface. Unlike the divergence (∇⋅v), the scalar product of the nabla vector (operator ∇) and the field vector (v), which is greater the more the two vectors are more aligned (closer directions, more parallel), the rotor vector (∇ × v) is the vector product of the two, which is as larger as they span a parallelogram of a larger area.

Consistent with this is the third Maxwell's equation, ∇⋅E = -∂_tB, which express a greater circulation of the vector field (E) equal to the opposite change of the magnetic field (B) with time (t). The fourth and last Maxwell's equation, ∇ × B = μ₀(J + ε₀∂_tE), where the vector J is the current density and μ₀ = 4π × 10^-7 N/A² vacuum permeability, represents the circulation of the magnetic field, also consistent with the principle of least action, otherwise confirmed in all the equations of physics known today. In this case, the square of the velocity of electromagnetic waves c² = ε₀μ₀.

Newton's third law (1686), actions and reactions, says that two bodies in interaction apply forces that are equal in size and in the opposite direction. Everything related to Newton's laws can be reduced to Euler-Lagrange equations (1750s), which in turn are derived from the principle of least action of physics, so they are indisputable from the point of view of the principle of least information. If these differential partial equations are unclear to you, the reaction to action is easier to understand as opposing the force to the force, which prevents too much oppressions.

The essence of the natural tendency to inaction, or minor action, sounds paradoxical, but it is in a quick and adequate reciprocal response, the consequence onto the cause. This can be understood as a "dance" deduction, but also as a very consistently implemented "tit-for-tat" tactic. Namely, deductions do not "rush" into uncertainty and that is why we can consider that they stay away from superfluous information, and the tactic "bad with bad and good with good" is a good path to stability.

Interaction »

Question: How do you explain the interaction with the "information field"?

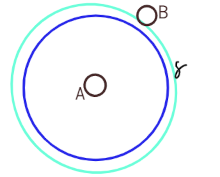
Answer: I will describe one of those ways, the application of that (hypo) thesis of "attracting" the current of electrons (Current), which I am reluctant to talk about, and which is so packaged that it resembles Feynman's diagrams. I don't know how "real" it is.

In the picture on the left are electrons A and B with a part of the "information field" around the first one. These are two consecutive virtual spheres (photons γ) in propagation. They start from one center (A) and therefore each of them is simultaneous for itself, and therefore it is quantum entangled. The distance between adjacent ones is the wavelength (λ), which does not change, for example, due to the constant speed of light (c = 300,000 km/s).

The surface of a sphere grows with the square of the radius, with which ratio its amplitude is "diluted", i.e. the density of the probability of interaction with another electron (B). If there is an interaction, then this story begins. The leading sphere disappears from the image, it transmits its uncertainty as an outcome to another electron, information is transferred, communication is performed.

The part of the distance between two electrons for the amount of one wavelength of a virtual photon (sphere) disappears, which we physically understand as the transmission of a momentum (p = h/λ) which is inversely proportional to the wavelength and directly to the Planck constant (h = 6,63 × 10^-34 J⋅s). That first effect is the mentioned attraction of electrons.

However, the virtual photon becomes real by interaction. The wavelength is the "blurring" of its position, and if it is longer, it will be less likely to find a photon in a given place. The loss of one virtual wavelength between two electrons is the appearance of real information between them, the greater the length the greater the information, so the "principle of information minimalism" and the rejection of electrons occur.

The mixture of these two, greater attraction by the loss of greater wavelength and then, the principled greater repulsion due to denser communication, is manifested through the induction of electricity into magnetism.

My explanation of the Compton Effect (Space-Time, p. 34) is a confirmation of the part of this story about the blurring of positions, and further, notice, it can be applied to the interaction of the virtual spheres of electrons themselves. But, I emphasize, the idea is quite crude and awaits a lot of testing.

Perceptions »

Question: As "same and different", what did you mean by that, is that a contradiction?

Answer: In different observations, there will be no contradictions in the perceptions of "the same", as long as it is about the experiences of various subjects. If A and B are mutually observed, and B and C are observed, then all three (A, B and C) are some realities. It is a possible system of existence and is in line with the multiplicity of information. That part of this theory is not quite new (Truth Vs Perception).

For example, parallel lines from "reality" are equally distant everywhere and do not intersect anywhere, but projected on a plane of paper can have a crossing at a close point. We call the points of intersections in descriptive geometry "points at infinity", or "ideal points", and their existence does not mean that this geometry is in contradiction.

For another example, I will cite the sinking of the body into a black hole. To the outside observer, this process is limited in time. Sooner or later, after a finite duration, a black hole swallows the body. From the point of view of the body itself, the "same" process takes an infinite amount of time, it never ends, because the body's own (proper) time flows more slowly (for a relative observer) so that falling into a black hole never ends.

The third example is the universe, the opposite is the second. From the point of view of us, or any similar "external" observer, the beginning of the universe was the Big Bang, which we see happened about 13.8 billion years ago. However, if we were to travel backwards in the course of time towards the beginning of the "creation" of the universe (we calculate by integrating, adding part by part of the proper persistence), the alleged journey would take an infinitely long time.

The third example was from "information theory" and let's take it with a grain of salt. It follows, above all, from the preservation of total information, the broader law of its conservation, and its spontaneous reduction in the present, i.e. the growth of the entropy of the substance (Growing).

Question: Do you have an example of the perception of quantum entanglement?

Answer: Yes, let's say with a virtual sphere (photon) expanding from the center of force (electron), which makes up one present.

Due to simultaneity (consistent with my theory of information), such a sphere is an example of quantum entanglement, and because it is able to separate the past from the future (interior from exterior), it forms a complete 4-D "world" (Dimensions), i.e. a deterministic order.

The law of conservation of information, and therefore probabilities, will determine less and less specific probabilities, probability densities, parts of the sphere's surface. They decrease with the square of the radius of the sphere (they dilute with its growing surface), and otherwise represent the decreasing chances of interaction of the sphere (virtual photon) with the corresponding other subject (electron).

When (if) interaction occurs, all the uncertainty of the sphere becomes certainty, possibilities become one of the necessities. What would be called in quantum mechanics the collapse of the quantum state superposition is happening. According to the theory of information, this is how observables are formed, and the outcome results from probabilities. At the same time, the entire present of the virtual sphere (photon) collapses and the 4-D deterministic version disappears, because the other electron does not recognize it. There was no compromise between those two worlds according to our wishes.

World A has disappeared, there are no observations between A and B, even if B and C have communicated, it is not worth it, there is no reality for all three (A, B and C). Communication changes the perceptions of both subjects.

The point of communication is that we do not have what we need, and the problem of this world is that it does not manage to satisfy everyone's needs. The perceptions of the subjects are so demanding, different and irreconcilable that each construction to one is destruction to some other. Their processes never calm down, although resting is exactly what they would like.

Question: What, then, is objective, if subjectively so dominant?

Answer: My first idea of Information Perceptions was actually to test the possibility that "objective" existence is a kind of illusion. This can be seen from my booklet "Nature of Data" (Novi Glas, Banja Luka, 1999), which I do not have digitally, entitled "Part II: The World Subjectively", pages 29-44. It deals with George Berkeley's the "Treatise Concerning the Principles of Human Knowledge (1710)" and his famous sentence "To be means to be perceived".

Quantum mechanics supports this idea, where "objective" existence is generated by a multitude of "subjective" perceptions and a combination of the laws of nature (mathematics, physics and others). At the lowest level of that multiplicities, in the micro world of physics, when a single interaction becomes everything from perception, and the world of the objective remains naked, it is shown how this strange Barkley's idea could pass.

Deduction »

Question: How to criticize deduction?

Answer: The answers to the questions from the intelligence test, like the one given on the left, are not from the home of deductions as much as they are the domain of associations. If you are a good chess player, mathematician, gymnast, or skilled in any field, notice that the best decisions are not (always) a matter of deduction, but often of intuition, something that "we have in us" and eludes official logic. The third example of this peculiarity is the advancement by the trial and failure method, the Monte Carlo method, or as Slime molds do.

By the implication "A ⇒ B", the algebra of logic writes deduction: "if A is then B". The first is the assumption, the second is the consequence. It is false if and only if (iff) assumption (A) is true and consequence (B) is false. It follows that "¬A ∨ B" is the same deduction now written by disjunction ("or" operation) of the negation of the first and the direct second statements. Otherwise, a mathematical sentence is an expression, statement, or value that can be either true (⊤) or false (⊥), there is no third. This is binary logic and is the basis of the first, el-computers.

Due to the higher speed of work, we also use polyvalent logics (true, maybe, false), with one or more different "maybe" values, but there is a theorem that states that any polyvalent logic can be reduced to bivalent (true, false). Therefore, the limitations of deduction of one of these logics apply to all others.

We often find the deduction powerless in terms of the real truth of what it finds to be true. Namely, if statement A is not true, then the sentence A ⇒ B is true whatever statement B. In other words, from the fact that the deduction is true, we cannot know that the consequence is also true. It is a paradise for liars, fraudsters, for manipulation in politics, the market, or law, and it is a great support, or so it seems to them, to many who believe that the real truth is unknowable.

However, when the deduction is not correct (not true), then it is certain that the assumption is correct and the consequence is incorrect (is false). This defines the implication and greatly confuses its users. For the more skilled, it opens a new "door of truth" and shows the way to a slightly more difficult and further way of research, so far "reserved" mainly for mathematicians. It is a "method of contradiction", discovered in ancient Greece. Mathematics came into being with it.

Due to the importance of contradiction, we are persistently (despite the requirements of the client of curricula) in trying to explain it to at least better students. This is usually based on the proof that the diagonal of a unit square cannot be represented by a fraction, rationally, i.e. that the root of number two cannot be written as the quotient of two integers.

Question: Remind me, how does that proof go, that √2 is irrational?

Answer: I'll retell it. The diagonal of a unit square with its two sides forms a right-angled isosceles triangle. It is the hypotenuse of the squared length equal to the number two. The Greek Pythagoreans believed that all the values of the cosmos could be represented by integers, or at least by quotients of such numbers, elements of the set ℤ = {..., -2, -1, 0, 1, 2, ...}, or from the set of rational numbers ℚ = {m/n | m, n ∈ ℤ ∧ n ≠ 0}.

Suppose that the root of the number two is rational, that √2 = m/n, where m and n are some integers of a reduced, truncated fraction. By squaring we find 2n² = m², so m is an even number. It is of the form m = 2k, where k is an integer, and then n² = 2k², which means that n is also an even number. But this is a contradiction with the assumption that we have a reduced fraction, that both, numerator and denominator, are not even numbers.

When the deduction is incorrect (here it is a chain "if it is then") we know that the assumption is incorrect, that its negation is correct, i.e. the root of number two is not rational.

Question: Do you have any more examples, some simple, or instructive contradictions?

Answer: Yes, such is the whole class of claims derived from Russell's paradox (1901). The most famous would be about the existence of the "almighty force", and they start like this. If there is such an "omnipotence", it could create such a heavy stone that it could not lift it itself. But if she can't lift something, then she is not omnipotent, so there is a contradiction. The conclusion is that there is no unlimited power.

I say that this is the beginning, because the term "stone" can be replaced by others, varied and abstracted, which would result in new contradictions and interesting claims. At the same time, "omnipotence" can be substituted. When we replace it with "the set of all sets", here is the proof that such a universal set does not exist. There is no set of all sets and that is why in set theory, in order to avoid its contradiction, we work only with the "universe" which contains just enough sets needed for a given task.

Many mathematicians worked out Russell's idea, including himself, sometimes very extensively. It is attributed to him that he demonstrated it with the story of "the barber who shaves all those in his village and only those who do not shave themselves" (Barber paradox). The question "who shaves the barber" reveals a contradiction and also leads to the proof that there is no set of all sets.

By abstracting here, when we talk about a set that contains everything, we are also talking about those that are not their elements, R = {x | x ∉ x}. From R ∈ R it then follows that R ∉ R, therefore a contradiction and a conclusion that there is no such set. However, from the conclusion R ∉ R follows R ∈ R, again with a contradiction. In other words, we cannot assume that there is a set R, but if we give up, it turns out that it exists, and that we should include it in a possible "set of all sets", and then we start from the beginning that it cannot be. That is Russell's "paradox".

Question: Interesting, I think I understood. Can you explain to me Gödel's theorem of impossibility, which you often mention?

Answer: OK I will try. The one I "mention" is one of the two theorems (Gödel's incompleteness theorems, 1931), both of which are his. In the beginning, Gödel kept only arithmetic, then algebra, with an idea that easily spreads and abstracts to the imagined universal theory, let's mark it with T, with (all possible) truths and only the truths.

By assumption, Theory T contains all the truths that can ever be revealed and contains nothing but the truths. We can imagine it as a "mind" that utters only correct sentences and everything that is true it can say. We can already see from this that this story is one of the sub-stories of Russell's paradox, say those about the impossibly heavy stone, and that is enough to see the conclusion that the omniscient "mind" does not exist.

In order not to repeat ourselves, however, we are going a little differently. Creature T cannot say "2 = 3", because it is an incorrect sentence. It can say that "it can't say 2 = 3", because that is the correct sentence. The paradox now is that the supposed omniscient creature T can talk about something that doesn't exist, from which it follows that it has it, and then again that it can't talk about it, and that it doesn't exist. This is Gödel's paradox of omniscience.

Question: Where is there the information theory?

Answer: We have seen that the idea of "omniscience" is contradictory, as is the idea of "omnipotence". Let's vary them now by replacing "truth" with "exist", which I often do in (my) information theory. I remind you that information or action, and then a physical phenomenon, cannot exist at all if we prove that it cannot exist. That is why the mentioned substitution is natural, possible, because "existence" and "accuracy" are equivalents (there is a mutual unambiguous mapping between them).

It follows that what exists, what we consider to be reality, is not everything that exists. No matter how large a set of phenomena of reality they had, imagined, there will always be them outside that set. No matter how much accuracy you collect, new ones will always be able to appear. This is the information theory I am talking about, the essence of which is uncertainty.

In such, the universe (whether six or more dimensional space-time) is not a warehouse of predefined possibilities from which our (or any) present can choose different options for its future, but it is a universe in constant creation (Creation).

Deduction itself, on the other hand, is a more modest part of that story. It travels through the static world of truth, I paraphrase, like a train on a previously established network of its iron rails. It is not able to cope with all the uncertainty, true unpredictability, or real originality, in discovering such truths that would not have already been traced within a given theory.

However, even as it is, deduction can be Eldorado for the first automata whose "intelligence" we will admire, until even better ones appear that would really surpass us.

Tilings »

Question: Is there never the same infinite duration of universe in contradiction with periodic structures of matter?

Answer: They are not. The question is very good, and by means of tiling I will try to explain it. It is possible to pave the plane by equilateral triangles, so that it looks the same everywhere. Such, periodic, coverage also achieve squares, then regular six-sided polygon, and then similar figures that can be obtained from them.

But the non-periodic coverage of simple figures is also possible (The Infinite Pattern), as can be seen in the image left. This already have the answer to the given question, that these two do not have to be in contradiction, i.e. that mathematical models that would avoid such contradictions exist.

It is a geometric way of considering this problem. Algebraic would concern the feature of irrational numbers (Continuum). When an infinite array of decimals of the real number is repeated periodically the number is rational, and when the decimals are of non-periodical values the number is irrational (Waves). The first make the so-called discrete sets with no more than countable infinite many elements (ℵ₀), while the infinity of the second is of the higher order and we call it a continuum (𝔠).

A number of positions of decimal places in the real number is countable, discreet, as well as a set of natural numbers. When an infinite subdivision of decimal places can be given at least two different digits, then the number of numbers can constitute a continuum of different values, as well as a set of all real numbers.

We notice a form that also applies to the coverage of the plane. Non-periodical overlaps can be on the infinite places continued on at least two different ways. Analogously is with reality. The reality is discreet for arbitrary observer (Dualism). It is also for countable infinite of them, but the number of options is a continuum. The template taken from the theory of numbers, on who knows how many ways, shows beyond its own field (Values).

The second question is why reality, in addition to continuum, are almost without exception to end in discrete gatherings. I would not have detailed about the reasons for our observation of reality in portions (Packages), the law of conservation information and immediate consequences, because I believe that you are already noticed them, as well as the answer to the given question.

Stability »

Question: We know what the advantages of stability are for the development of life, society, economy, but what about its disadvantages?

Answer: Stability is spontaneous immutability, but there is absolutely no such thing, at least as far as the "universe of uncertainty" we are going to talk about is concerned.

We know that the parameter (prototype metre bar) used from 1889 to 1960, the iridium and platinum alloy rod, as well as the international prototype kilogram — have changed over time, both measures carefully guarded and maintained — so how can we continue to believe that something less strict kept better preserved. Today, we believe in the immutability of natural laws, but that is also a question of how long.

So, the first problem with "stability" is the suspicion that such a something is actually an ideal that does not really exist. That is, that we can only deal with approximate and always temporary "immutability". In doing so, we note that what applies to "stable states" will also apply to "stable processes" and vice versa, due to the state-process dualism (Dualism).

An object or change can, so to speak, be plunged deep into a state of "stable" balance and it seems to us that it will never come out of it on its own, but that is seemingly. There must be either a change in the state itself or a change in the environment that will lead to a change in the broader view of that state and finally to a change in the state itself. This is how obsolescence occurs (Obsolescence).

Then why not manage change, you ask, to avoid obsolescence? The answer is simple: because of the objectivity of uncertainty. The chances that we will "manage well" are limited. There is no absolutely good consequence management, due to the same state-process duality. Every management process is subject to mistakes as well as the stability of something "concrete".

It seems that nature does not tolerate stagnation (immutability) and if that is its principle, then we can "harness" it in the same desire. Let's find the right state of balance and the development of life, society and economy will happen spontaneously from it. If we bring this state into the desired imbalance, if we accelerate changes, nature will resist that additional development, now due to the principle of minimalism of information, i.e. uncertainty, by its a new force (Action).

Everything in the world seems to have a fear of excess options, a desire not to have them, even though the whole world is of options, that is information created. However, living beings are such creatures that have a surplus of choices, more actions, than non-living beings of appropriate structure, that is, from the aggregate current information of the substance that makes them up.

In that sense, life is an "unnatural" phenomenon, like a storm that defies the principle of the least action of physics, or is like a geyser that flows against gravity. I deliberately emphasize this anomaly of the principle of minimal information in order to better understand the existence of life and the "natural" course of life towards death. It is a path from excess of uncertainty, i.e. greater vitality, to stability and calm, to less surprises and efforts.

There is also the main flaw of stability, in its deadness, boredom and lack of diversity that we love because we value life.

Tactics »

Question: Is game theory part of information theory?

Answer: Yes, if you don't really mean on the well-known math game theory. The Information Perceptions will agree almost completely with some results of that modern theory (Tit-for-tat), and let's say it will not agree to that extent with Neumann's (see in Capablanca).

Namely, looking at challenges as opportunities for action while preserving resources where possible — the information of the perception of a given competition becomes maximum, and thus its vitality. This corresponds to the "evil for evil and angelic with angel" way, which is at the top of tactics in the fight for victory, and, on the other hand, its ferocity promises extreme results in a theory in which information is everything.

In order to improve this information "retaliation" tactic, information theory could only recommend a dose of uncertainty, which is the essence of my theory. Blockages that occur in cases of mandatory return "good for good" or "bad for bad" would be avoided when a different (unpredictable) response could offer a better result. But it is also a place where these two theories could easily agree.

It will also agree on von Neumann's "minimax" theorem. Let us remind ourselves, in cases of open play, it speaks of the superiority of the tactics of a player who would choose for his best moves those who would leave the opponent the worst choices. We do not agree only on the scope of the "open game", how interesting it is, present where we need serious tactics at all, and therefore how realistic it is. Even when there is openness of moves, as in chess, then it is fictitious due to the time limit of the players.

A lie is a hidden truth (Dualism of lies), so disinformation, manipulation or deception have their tactical value. Actions, and then information, are kind of true, because what we could prove to be incorrect could not exist. But the reasons for "information perception" teach us that "fraudulent methods" are not first-league games.

They are supported by the fact that a dose of lies is more attractive than pure truth, as well as exaggeration with untruths. This is firstly because of the lack of information (the principle of minimalism), and secondly because the building is weak on a weak foundation. Pure truths are more lasting, they will not change, as will the rules or situations with fewer options. So, in the long run, but slowly, the truth defeats the lie — again due to the principle of minimum information — every lie, and easier the one that is too big. In addition, harder lies burden the strategy of the liar more, make it harder for him to assess his position, and make it easier for him to force bad moves.

Note that we are talking about game theory not from the standpoint of classical game theory, although we find the conclusions acceptable to both. Read in my recent answer (Dilemma) that there are borderline tactics between "games of victory" and "games of balance", such as the "prisoner's dilemma". Their basis is the uncertainty due to which such divisions belong to information theory.

Finally, tactics and strategy are not the same. "Tactical initiatives typically solve pressing needs, such industry updates, breaking news on the competition, or the latest product information." — writes in the article on the application of this well-known theory in economics (Sales Performance) and further — "Strategic initiatives maximize the significant investments made by an organization in training, sales processes, and coaching. Strategic needs lurk below the radar and often go unnoticed, yet when strategic needs are addressed, they can create significant performance gains for the company."

These are good observations from the point of view of information theory as well. With short (tactical) steps, the best moves can lead us into a trap, and into losing the game. An example of this is the cunning way of a game hunter, or the saying that the road to hell can be paved with good intentions. With long (strategic) steps, it is possible to win with sacrifice. We expect this value in the economy when we want to win later by investment, or chess players in the opening of the gambit (with the sacrifice of the figure). Moreover, almost every "lose-lose" tactic will win the "win-win" tactic.

The latter, as well as "gain-gain", or games of unconditional non-reproach, compromise and games of "gooders" in general, are just an excerpt from "reciprocity" (tit-for-tat tactics) and are therefore weak. Note that the predictability of "good things", i.e. less unpredictability, is also a confirmation of their weakness, i.e. less success of these tactics in competitions. Their eventual advantage in development (Stability) must therefore be protected by additional coercion (states, morals, promises).

It is similar with the games of "evil", i.e. pure predators, selfish or irresponsible in return for "good for good". We usually overestimate the scope of such, for example, by interpreting Darwin's evolution. If we look at the "survival of the fittest" thinking wrongly about what should be best for survival, we will be surprised by the prevalence of empathy in the biological world around (Evolution).

Democracy »

Question: Are you a critic of democracy?

Answer: I would be a critic if I was interested in that topic, maybe, but this way I am just an analyst. There are some regularities in the course of democracies, which are obvious to some mathematicians who do not deal with democracies and completely invisible to others who should deal with it.

These are transformations of equality into inequality, with very special regularities. They can be traced, for example, in the well-known theory of free networks, or in the still unknown theory of information. In the terminology of the first, this means that the pursuit of equality of node connections and greater network efficiency necessarily leads to an increase in inequality between nodes. There is a decreasing number of nodes with more and more links (percentage), compared to the growing number of nodes with rare links (Value).

In practice, this is the fundamental reason why the free market of money, goods and services is spontaneously developing into a decreasing number of growing holders of the three, compared to more and more of them who lack it. This is basically the concentration of the power of the Christian religion (equality of people before God) in the churches and finally to the Vatican, or before that, for example, in the growth of the Roman Republic into the Roman Empire. We have examples of that regularity everywhere, wherever it is possible to define some equality, because its further development is a matter of mathematical certainty before these-or-those so-called socio-historical phenomena.

I have not yet seen a historian deal with that kind of necessity, although there is no example where it has betrayed expectations (unlike popular speculation where anything over 50 percent would be good).

Question: How do you use information theory to explain the tendency of "free networks" to have fewer and fewer nodes with more and more links?

Answer: Equality translates into efficiency, or, if it makes sense to speak in that way — into security, into a decline of vitality. A given number of outcomes has maximum information when they are equally likely (Equality). Going principally towards less information, striving for greater probability, such a system can develop into less informative and that happens.

This is how legislators happen in societies on the transition from youthful intemperance to senile serenity. Babylonian king Hammurabi (Hammurabi Code), Suleiman the Magnificent (Suleiman the Lawgiver), Dušan of Serbia in 1349 (Dušan's Code), the European Union (EU legislation) — there are well-known examples of extraordinary breakthroughs in this regard.

Degeneration »

Question: Democratic values disintegrate spontaneously and then where is the end?

Answer: Society loses information and becomes easier prey for more vital newcomers. This has happened to many civilizations. They became "too" focused on internal organization (Information Stories, 1.4 Feminization), and in a "dangerous" environment.

A different continuation is that they enter the "trap" of evolution in a spiral process and be preserved like Crocodilians (250 million years old), Velvet worms (505 years old), Cow sharks (at least 409 million years), Horsetails (300-360), Lice (130 million years), to name just a few of those long-lived and otherwise rare species.

It is unlikely that homo sapiens could now be so easily "frozen" in time, and besides, it is not very important to us today. At this moment, we are facing the process of strengthening the economic power of fewer and fewer of them (Democracy) and, consequently, subordinating more and more once free goods to the value of money. Regardless of the apparent increase in the possibility of choosing a job, efficiency implies the absence of leisure. Leisure is the mother of all vices, it is not said in vain, but in some of them there is also creativity.

The rich and powerful will continue to strive to master the otherwise better science and technology for the purpose of supervising and controlling not only people. They will work on more productive ways of subordinating institutions in general, and especially the judiciary, government, and politics. Already now, corporations are more successful (and unfair) in making a profit that used to be a well-intentioned, generally accepted saying that health is most important to us, but it is not far off that they will go to food and water with the same intentions. Along the way, they will master the weather conditions and profit from the making of some sunny or rainy days.

Like the removal of male offspring in livestock breeding (kill male calves), I count on continuing to encourage the role of women, certainly to increase profits, but also in the secret expectation that in a more technologically advanced environment it will be easier to exploit them alone. These are spontaneous flows that will be difficult to stop just like that.

The proposal (Value) to give less importance to money, without shaking democracy in its very foundations, will be further and more than achievable. But that’s not worse than what can happen then. Individuals subordinate themselves to the collective by renouncing part of their freedoms, for example in exchange for "security", and they also gain reduced physical (Less Fit), mental (losing intelligence) and health abilities (dependent on medication), perhaps, simply because of adaptation to conditions where we do not need those abilities.

Life »

Question: How is life possible if it opposes the principle of minimalism of information?

Answer: First of all, diversity is also a principled phenomenon. Multiplicity (Vast Diversity) is therefore not a problem, but a solution. It happens analogously with all particles and bodies that accelerate equally downwards under the effect of the earth's gravitational force, but from them, and we can say because of that, geysers and volcanoes are formed. Storms are similar, despite the principle of least action.

Life is a kind of unrest (Information Stories, 1.5 Life) and we can consider it an anomaly. It has information (quantities of choice) in excess compared by the substance of which it is composed, although it still, in its own way, undergoes a principled reduction of information. No one still knows exactly how life originates, but we are already successfully assuming some of its processes (They Evolved).

The life processes in these models seem to us to follow the "principle of minimalism" while falling into the trap like a "dog chasing its tail". It is as if the types of vicious circles (Cycles) were created perhaps by the absence of transitivity of a relation that only resembles to the order relations.

According to the principled multiplicity of the "world of information", these processes should not be all from the "living world". The very pursuit of equality is natural in that world, as well as its opposite (Democracy), and these two again build a natural wave structure of information (Rebound).

In that sense, it is understandable, in a roughly viewing constant and in detail changing environment (like the terrestrial one), to expect the repetition of species, emergence and disappearance, not only of life traits, but also of life itself. Some of these have almost been observed, for example, long ago in large aquatic mammals and more recently in crabs (Evolution Crabs).

In the end, the substance of the geyser is pushed upwards, because that is the easiest way for it. To a large extent, this also happens with living individuals who would likewise to be deprived of excess action (information), but they have nowhere to go, since all the matter around them is filled, so they give their freedoms (options, vitality) to the organization. In this way, "spontaneously" an even higher form of "life" (Emergence) grow as a kind of paradox of the principle of minimalism.