August 2021 (Original ≽)
Cosmos
The cosmos (Greek: Κόσμος) originally meant order and harmony, unlike chaos (Greek: χάος), and today it is the universe, the totality of all living and non-living things. In information theory, as I derive it, there is no talk of the cosmos as a "totality," because it is forbidden by Russell's paradox of sets (there is no set of all sets) and Gödel's theorem of impossibility (there is no concept that would encompass everything). Also, the information theory itself expects that, no matter how big it is, the cosmos is also some information and, therefore, some uncertainty.
In information theory, as we know from the theory of relativity, 4D (four dimensional) space-time is part of at least some 6D space-time. In 6D we have 4D reality surrounded by pseudo-reality, and it itself (6D) is also some information, so I predict that it will not be the end of the story about the cosmos — some future cosmology. That future "cosmos" will have a part outside the "pseudo-reality" that is inaccessible to our perceptions. He may be called "divine," perhaps "phantom," or a third, but it is not the final "whole."
There is no "end of the world", because that is forbidden by Russell's paradox of sets, Gödel's theorem of impossibility, and (my) information theory itself.
Icy Sun
Question: Where do such stupid theories as this come from (Hanns Hörbiger, 1860-1931) about the icy sun?

Answer: If it is a question of learned people, then from a wrong assumption and consistency. For example, when we generalize the idea of spontaneous entropy growth with the assumption that stronger gravity offers states of higher entropy, then the "logical conclusion" is that stronger gravitational fields have higher entropy and that gravitational attraction is equivalent to spontaneous entropy growth. Just as heat spontaneously passes from a body of higher temperature to a neighboring body of lower temperature (another law of thermodynamics), gravity attracts, because then the entropy increases.
Higher entropy corresponds to a lower temperature, so based on the above generalization to gravity, the Sun has the highest entropy and it must therefore be as cold as ice. The author of this erroneous theory was long dead when the Nazis remembered him to add at least something else against "Jewish science" and especially to challenge and ridicule Einstein.
Question: In information theory you have also generalized entropy. What's the difference with this?
Answer: Unlike classical thermodynamics and, of course, the aforementioned theses that lead to the "ice sun", my generalized entropy applies to all substance (not space). It decreases with the strengthening of the gravitational field, and information decreases with its decrease.
For example, a body in uniform inertial motion has a lower relative entropy and therefore the body will not spontaneously transition from a state of rest to a state of motion. Because of the same, the Earth will not spontaneously fly out of its orbit and rush towards the Sun. Excess information that occurs due to less entropy (relative motion or gravity) is "apparent" in the sense that one's own (proper) information is in a parallel reality directly invisible to the relative observer.
Inversion
Question: Did you think that some conservation laws could also apply to space-time?
Answer: Of course, often. I have rarely written about it, because there are little chances for some physical experiments on that topic. However, it is not impossible to discuss some theoretical possibilities now.
In the theory of information as I see it, the course of the present is not symmetrical, since it is moving towards less informative states. Nor is space symmetrical in the usual geometric sense, because further points are further in the past (future) than the given, if they are viewed as part of a system that is moving away (approaching). However, all 4D parts of 6D space-time are equal in the physical sense. In this sense, according to Noether's theorem, the law of conservation of 4D space-time applies.
The law of conservation of space-time can also be defended from the point of view of conservation of action, whose quantum is a product of energy and time, i.e. momentum and position. Equivalently, the same is true for conservation of information.
From these positions, I considered the inversion of time (in the book “Quantum Mechanics”, p. 277-280, subtitle “1.4.1 Time inversion”). For example, timeless photons annihilate into pairs of electrons and positrons, whose sum of charges is zero, as well as the sum of spins, the sum of momentums and the "sum of time". In other words, positron time goes backwards.
One of the consequences of such an attitude, it seems, would be that antimatter (whose time flows backwards) is earthly, attractive to us gravity is — repulsive. So, I have been considering the options of the "law of conservation of space-time" for a long time, but I avoid writing a lot about it in public, because the idea is still rooted. I have too many controversial topics to burden my readers with one more, even worse than the others.
Conservation
Question: What does Einstein's formula E = mc2 have to do with the "conservation laws of space and time"?
Answer: This story (in information theory) becomes relevant again after the latest experiments, primarily those where it has been observed that photons (light) are transformed into pairs of particles-antiparticles and vice versa. One of the links is given in the previous answer (Inversion).
When a pair of timeless particles (photons) annihilate in collisions and create a pair of time passing particles (electron-positron), the conservation of the aggregate momentum, spin, energy, but also "space-time" is confirmed. Namely, the directions of the created particles are opposite, both in space and time, whereby their "flow velocities" are equal, because they are of equal velocities (impulses). Almost at the same time after annihilation, creation occurs.
Laboratories see in these collisions a confirmation of the formula (E = mc2) that energy and mass are equivalents, and I (consistent with information theory) that certain conservation laws apply to space and time.
Question: Where does this need in information theory come from?
Answer: Simply put, it is principled. Information is the ontological essence of space, time and matter, and the law of conservation applies to it. Therefore, some legality of "conserving the amount of time" also applies.
Question: Will such a "discovery" change anything in the story of information?
Answer: Yes, for example, I can now say more openly that a physical system whose relative time flows more slowly has some additional flow of its own (proper) time invisible to the relative observer.
Question: Do you view the law of conservation very broadly?
Answer: Yes, I hope so, if you mean its detection in physical phenomena where it has not been noticed before. For example, in spending the health of future generations by better treating the current (declining need for innate resistance), or exhausting the vitality of a rising civilization followed by its decline (more intensive internal organization of society is increasingly limited, reducing "quantities of options" make them vital).
This includes the initial increase in the amplitude of the flicker (particle-wave) followed by its decrease. But this way of observing known phenomena requires tracing by discovering some symmetry (according to Noether's theorem, maintenance follows from symmetry and vice versa), and then re-examining the method of measurement. For example, what is the measure of health of a given generation?
I am still not ready to enter that space completely, but I am aware of the possibilities.
Slowdown
What is more probable happens more often, or everything tends towards a less informative state, because that is the more probable. As the "flow of time" is always measured by the amount of past events, the attraction of a slower flow of time goes hand in hand with the previous one.
In a flood of "similar" nebulae, such a simple conclusion seems silly, but unlike the "others", it is not really possible to dispute it. For example, in the general theory of relativity, the slower flow of time gravitationally attracts. This is the sentence of Einstein himself after considering the solution of some of his equations, now, of course, we have it with a completely different meaning, seen from a completely different angle.
We further conclude that what is in a stronger gravitational field is increasingly lagging behind in the past of the cosmos, compared to the rest of the universe. And from the previous one, the universe is evolving into more and more "slow" (time flow), so these two currents seem to be balancing.
Yes — the answer is — and books could be written about the news. This is just a detail from that one part that I managed to capture (of course not in the order presented here). Finally, the present develops towards the future (and not towards the past) simply because the future is more attractive (slower).
Question me was: Does information theory have anything to say about the theory of relativity and what?
Regulation
The state of less information corresponds to the state of greater regulation. That is the essence of life and efficiency. Greater vitality is based on a greater number of options, has greater possibilities of action, but can hardly do without efficiency, stability and calmness, which pull to the other side.
Question: Less information goes with more regulation, you say, and does that also apply on a cosmic scale?
Answer: Yes, as far as we know the history of the universe today. For example, thermodynamic entropy S = Q/T, where in the numerator and denominator are increments of heat (Q, thermal energy) and temperature (T), at the time of the "Big Bang" and shortly after — it was smaller, to grow over time. This means that the temperature of the universe decreased more slowly than the heat. Entropy (S) grows spontaneously further, on which the "Second Law of Thermodynamics" is based, which speaks of the spontaneous transfer of heat from a higher body to a lower temperature body.
However, the position of my "information theory" is that as entropy increases, information decreases and regulation increases. The very fall of information with the law of conservation of information, I have often explained, means that the mentioned entropy (and the corresponding information) refer to the substance. Substance information spontaneously transitions to space information at a rate dictated by a higher probability of conversion of fermions to bosons than vice versa. The universe has less and less substance and more and more space, and that is why the universe is expanding.
So, the universe is expanding, space is cooling, and our own present surprises us less and less (uncertainties, the essence of information is less and less). At the same time, some discoveries (e.g. originally common electro-magnetic-weak forces) of differences in physics then and now, can be subsumed under "greater regulation" due to "less information". If this is accepted in physics as a possible interpretation of the same, it will be a step towards accepting these ideas of "information theory".
Natural laws
Question: The formation of natural laws is influenced by the "principle of information", you say. How?
Answer: In two ways, subjectively and objectively. It is a principle that speaks of the spontaneous transition of all physical systems to states of lesser information (higher probabilities), and thus of living beings. We recognize it in the need to avoid greater efforts and aspirations to calm us, that is, the sluggishness of all physical bodies.
That is why we love rules and routines, because that is how we reduce our intellectual exposure to originality, uncertainty and risk. It is the mentioned subjective influence of the principle of information, which forces us to "invent" natural laws, that is, to devise "formulas" for easier "understanding" and prediction of natural phenomena.
I called the second way "objective", because it has nothing to do with what we individuals think. As physical states tend to be more likely (less informative) the world becomes more certain. We are facing rules, that is, "natural laws", except that due to the slowness of the process, we cannot directly notice that.
Quantum entanglement
In the short answers to the questions, below under the headings “Quadratic form” and “Reaction to Action”, my earlier explanations of quantum entanglement in information theory are told in more detail and more extensively. This theory differs from standard physics in the fundamental uncertainty from which several space-time dimensions arise (at least six, three spatial and three temporal), then according to the information of perception.
In the first of these two topics (Quadratic form) quantum entanglement is interpreted almost equally in my way (the form of information perception) and classically. I deliberately took an example from the link in the text (Quantum entanglement) and interpreted it in the way of "information theory" so that "differences" are "barely noticeable". But when this explanation is analyzed a little deeper, additional differences can be noticed.
In the next topic (Reaction to Action), it can be seen that the similarity between my informatic and classical interpretation of quantum entanglement is actually even smaller. Deficiency of information, which creates entanglement, means deficit of action, and of course the absence of their transmission by "phantom action at a distance" — because between given (entangled) events there is an "observer" in relation to which two distant events are simultaneous.
This simultaneity is always possible in 6D space-time information theory, unlike classical 4D space-time physics. However, direct transmission of action, i.e. information, is not possible between parallel realities, so it doesn't happen.
Simultaneity
Question: Events are simultaneous when there is an "observer" in relation to when they are simultaneous. I don't understand why you complicate the notion of "simultaneity" so much and what is it for?
Answer: In the special theory of relativity (1905), observing a moving train from inside and from the embankment, Einstein showed that two observers do not have the same "present". However, in the same, he showed that there is a unique present of each of the relative observers of inertial systems in uniform motion. That is why the issue of "simultaneity" is complicated.
Then, in the general theory of relativity (1916), it is revealed that within the 4D space-time of Minkowski, there are no unique, at least different present ones. If we include "that" in which gravitational space is curved, and for that we need the assumption of "objective uncertainty", i.e. "information theory" in the way I develop it — there are unique "observers" (physical systems) in relation to which any two events simultaneously.
I have written about it many times, even in this blog.
A further question is why it is necessary to have simultaneous observers, and one of the answers is quantum coupling. Read the attachment as well „What is quantum entanglement?“, so imagine the decay into two photons of a particle of zero momentum and spin. Due to the law of conservation, it decays into photons of equal momentum but opposite directions of motion (say left and right) and spins (+1 or -1).
The spin value of the left as well as the right photon is completely random and unpredictable, but due to the law of conservation of spin, whatever the left, the right must be the opposite. Let's imagine that after a long time, these photons travel very far, but right where, on the left and right side (from the mentioned decay) one on each side laboratory is waiting for them, where their spins will be measured. The distances for the measurements are prepared in advance so that the work will be completed before the information about the result could reach from one photon to another.
Of course, similar measurements are already being made and they confirm what the calculation of quantum mechanics gives. And that is that every time two spins of such photons are opposite. It turns out that the spin of each of the photons is completely random, but it still isn't, because each of them is always exactly synchronized with the other.
This is where the need for the objectivity of a single observer of simultaneity arises. The topic is "difficult" because it is still not in physics, but tomorrow, when this is discussed in elementary courses (I believe), the students at the time will consider these explanations trivial.
Quadratic form
Question: Are quadratic forms and coupled quantum states types of information perception?
Answer: Quadratic forms are a special case of "information perception" S = xu + yv + zw + ..., where arrays (x,y,z,...) and (u,v,w,...) are multiplied. It can be said that, I think.
In the figure on the right, in the first row, there is a biquadratic form, defined by a symmetrical matrix of the second order (factor in the middle) and the same vector (x, y), covariant and contravariant, on the left and right. The next line is a generalization to different vectors left and right. The symmetric matrix can be diagonalized (here into a unit one), so that a characteristic form of perception information is obtained.
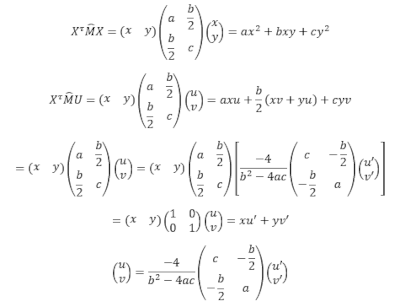
As for the second question, when the sum of the products S represents a entangled quantum state, the answer is the same as in quantum mechanics. Then when the factors are such that they do not allow the simple separation of the sums into the product of the arrays.
Question: How do you explain quantum entanglement?
Answer: The mentioned series represent the superposition of quantum states (Born rule). The components of the array define the probability distribution of independent random events (the chances of measuring a given property) of the total sum of one, which means the certainty of the occurrence of one of them. The absence of the possibility of forming all members of the sequence, i.e. reducing the number of options, means increasing the probability of individual and reducing the information. That in turn means increasing certainty.
For example, if we have components of the first vector that determine some state A and the corresponding second for state B, pure states (quantum state) bosons S = xAuB - yAvB, according to the modern interpretation of quantum mechanics, the entropy of the subsystem will be greater than zero (Von Neumann entropy), which according to (my) "information theory" means that the information will be smaller, and with it the arbitrariness less.
Note that this (my) explanation is more convincing than the official one, which in the "transmission of action" in order to synchronize and conservation, say, the total spin, "swallows" (misses) the non-transmission of information. When we have two boxes with one left and one right glove, and we don't know which one is in which, so we open one of the boxes immediately, we know which glove is in the other box, no matter how far apart the boxes are (Einstein's example, here to confirm non-transfer of information).
A further explanation of quantum conjugation here and classically agree (Quantum entanglement) and there is no need to repeat it.
Reaction to Action
Question: Where does the law of conservation of information come from and why is it quantized?
Answer: The law of conservation of information also comes with "belief in experiments", but its stronger confirmation is the reversibility of the operators of quantum processes. That free information travels at least in packets (quanta, atoms, whatever) follows from the contradiction between the assumption of its infinite divisibility and the established law of conservation. Namely, by definition, a set is infinite if and only if it can be its proper subset.
Question: Then is a possible reaction the opposite and of equal intensity of action?
(We are talking about the emission of a virtual photon from a given electron, which may or may not interact with another electron, and sometimes when that happens, the alleged photon will be realized, transmit its energy, momentum and spin to the other electron, so the question remains how to of that knowledge comes the starting electron, which complements it and complies with the laws of conservation.)
Answer: Let's be clear, the quantum of action is the smallest amount of "free information", but I do not claim that it is the smallest amount of information at all. A quantum (a photon, for example) has parts such as position, moment, frequency, and similar information, but it cannot have, say, a "position" without others.
This is in line with (also my) thesis of "pure uncertainty" (the smallest package of free information), the smaller part of which, which has less uncertainty, must have more certainty. In other words, smaller and smaller parts (of the least information) are less informative, less and less random in nature, and more and more causal.
Second, the process of reaction to action, from the supposed future to the past, can be explained by "time machines", i.e. particles that go backwards in time, but there are also alternatives. Losing a virtual photon, the first electron becomes a more likely target of a similar photon of the second electron and, finally, the two electrons bounce like two boats on the water after throwing a bag of sand from one to the other.
Question: What is the "alternative" to this interpretation of the reaction to action?
Answer: Slowly, I will explain, but that part of my information theory is also unknown to the public and it is not worth rushing. Before that, let's consider one well-known example with two cups of equal amounts, in the first coffee in the second milk. From the first cup, transfer a part of the coffee to the milk with a spoon, and then return the part of the liquid of the second cup back to the first from the mixture with the same measure. The question is, what is more in the end, milk in coffee, or coffee in milk?
Let us now imagine that the past and the future are the two mentioned vessels with slightly predefined contents. The initial uncertainty is realized in the certainty of an equal (quantity) of information. They are like the situation before and the outcome after the roll of the dice, where the "certainty" of the sender is again the "uncertainty" for the recipient. There is no "news" sent another time (which would no longer be unknown to the same recipient), but it is always real news (unexpected) for a new recipient.
Then we notice that at a given moment in the past, whatever the first electron had, it would no longer have in the next moment. On the other hand, whatever it lacks, what it can absorb (we would say more information-wise, what it can communicate with), it will get in the next moment, because it is in an endless sea of other electrons. Another electron, which will, for example, take over the virtual photon of the first electron, constantly sends virtual photons around itself and immediately fills the possible lack of the first one. At the same time, "immediately" means that there is some "observer" (some point of view) for whom both electrons are simultaneous!
This "phantom simultaneity" is an unacceptable idea for classical physics, because it does not work with three spatial and three temporal dimensions with the possibility of choosing any four of them six for some "reality", as (my) information theory. In addition, we note that this "alternative" explanation of "reaction to action" also explains the simultaneity of quantum coupling (phantom action at a distance, as Einstein called it).
Continuum
Question: The world is constantly changing and if it lasted indefinitely, all its combinations would work out?
Answer: Incorrectly! It is a "deduction" with which even the best physicists can make mistakes, and recently it was a great turning point in mathematics. See for yourself a more detailed explanation in the attachment, in the book “Multiplicities” (Differences, p. 11-13), that I don't have to repeat that known part.
A series of decimal places of a real number greater than zero and less than one (0,abc...) has "correct" countable infinitely many positions. They form an ℵ0 (aleph-zero) infinity level, which represents the amount of natural numbers, even numbers, integers, fractions. However, varying digits (a, b, c, ...) with at least two possibilities in the binary case (0 and 1), or ten possibilities of decadal notation (0, 1, 2, ..., 9), anyway, we get an innumerable infinity called a continuum (labels 𝔠). Infinity is generally denoted by ∞.
It is not possible to encode real numbers with natural ones, or more precisely it is not possible a bijection (mutually unambiguous mapping) among natural and real numbers, i.e. it is not possible to "enumerate" real numbers, so we say that the (cardinal) number of real numbers is a continuum, an infinity of higher order than aleph-zero.
But, no matter how we define the short interval of real numbers, by adding them along the real axis, we will string the most countably infinitely many of them. Although, I repeat, there are many more real numbers. The consequence of this is that the moments, the intervals of time (quantum of action, products of energy and time), can be the most countable infinitely many. Then, since many situations have at least two outcomes (the principle of objective uncertainty), the number of all possibilities is at least a continuum. From the relative point of view of several coordinate systems, the so-called "Observers", who are always for the same state, the number of possibilities of one reality is also a continuum. These two modes, both somewhat abstract, are species-like pseudo-realities, the first 6D and the second 4D space-time.
Therefore, from the point of view of one coordinate system, there are too many events of 4D space-time of all observers, as well as events of 6D parallel realities, for everyone to be able to stand in one infinite series of cosmic moments. From the point of view of one observer, it is not possible to have a continuum of actions (particles) of one "present" of any space-time, so that is not possible for such a person even in a countless infinite series of space-time. This is, I repeat, because the set of pairs (x,y) or triplets (x,y,z) and so on is also countably infinite if the elements of the array x, y, z, ... form countably infinite sets.
The set of possibilities is a continuum infinite, so the multiverse (at least) is a continuum. With this we come to the justification of an ancient realistic-mathematical philosophy (I don't know if it exists as a consistent system) which says (I think hypothetically, if such a philosophy does not exist) that what is beyond our power is objective. What we cannot change is less subjective than "because of us changeable", so all mathematical theorems and especially those about infinities are objective.
Therefore, e.g. exists Benford's law, the law of the first digit, which claims that the appearance of numbers derived from real life, the distribution of the leading digit follows a specific, non-uniform distribution of probabilities. It is unusually reliable for testing, for example, bookkeeping, in decisions whether the invoices are written "from the head", i.e. tuned, or come from the actual business (regardless of whether the company has earned or lost).
This is because there is much more to what we can imagine than what would actually happen. That is why, I believe, it is information theory (see Infinity) a step forward in understanding reality.
Popularity
Question: Can any example of information perception in popularity?
Answer: Can. The YouTube audience asks the best entertainers to be silly, original, to do something that no one before them is, a specialty. A similar surprise raises the ratings of the media itself. We define the values (rating) of both, the higher the value, the greater the popularity, so we calculate the information of perception S = ax + by.
Suppose that according to some standard, within the given areas (say classical and popular music), the values of our YouTuber are a = 3 and b = 5, and the medium itself has values in the same respectively x = 4 and y = 7. The fun of the program (perception information) can then reach the value S = 3 ⋅ 4 + 5 ⋅ 7 = 47. If the rating of another YouTuber is reversed, a = 5 and b = 7, his performance would have the value S' = 5 · 4 + 3 · 7 = 41. So S > S'.
So, the vitality of the performance is greater to the entertainer who gives more in what he is better at!
Investment
Question: Do you have any economic example of information perception?
Answer: Yes. Imagine having two locations A and B for building a business facility, the former three times more profit-effective than the latter. Divide the budget into two parts X and Y, three times more in the first than in the second. When you invest a more profitable object better, and the other worse, the expectations are S = a⋅x + b⋅y = 3⋅3 + 1⋅1 = 10, and if you invest more in a worse investment, the expectations are S' = 3⋅1 + 1⋅3 = 6. Obviously S > S' .
However, there is a connection between greater "information of perception" and the success of "tit-for-tat" tactics.
World of Lies
Question: How do you think that the "world of truth" is equivalent to the "world of lies", is it an excerpt from a fairy tale, a story, or is it a reality?
Answer: It is a reality, albeit not yet recognized in mathematics. The discovery comes from "information theory", from trying to understand (find a contradiction) in the assumption that information is the ubiquitous tissue of the cosmos.
Namely, information is a reality, and as such it cannot happen if we can prove that it cannot happen. So, information, like any physical event, is true.
The problem then arises with the question: then what is a lie? Does a lie even exist in the sense we consider it today (as something that will not and cannot happen), and the way out of that paradox comes with the help of the "principle of minimalism of information". Namely, nature tends to realize more probable events more often, which means less informative states. Nature is made of information, but it seems to be "ashamed" of it. A lie is hidden information!
Then I needed independent, mathematical proof of the above statement, without "information theory". And indeed, it was in front of everyone's nose, imperceptible. Let's pay attention to the truth tables (Truth table), say a total of 16 binary logical operations such as conjunction and disjunction. We can map them by bijection (double-sided unambiguous mapping) by translating "true" into "false" and vice versa. We get a set of those same tables, shifted names.
Every starting tautology (a statement that is always true) in these "new" tables becomes a contradiction (a statement that is always incorrect) and vice versa. In that way, knowing the contradiction (by mapping backward), we get a tautology, and that is actually a procedure that was done in mathematics (by the best ones) a long time ago. Thus, for example, the Pythagoreans proved that the root of the number two is an irrational number, or Lobachevsky who find a non-Euclidean geometry, named after him.
It follows that a lie can be "unpacked" (understood, deciphered), as well as the truth, but a little harder. Example in the video link “How Many Liars Are At The Party” shows that this is possible even in the "most difficult" case. It also follows that lying skills could be considered higher levels of intelligence than the (average) human. I do not mean the gossip typical of some politicians, managers, or lawyers, but far more complex, subtle statements (for example, tell me a short story consistently, your true experience from the summer, but so that each sentence is incorrect).
Dualism
Question: Can you briefly and simply explain quantum mechanics to me?
Answer: This is considered impossible, but it is not forbidden to try. At the beginning of the 20th century, when the first quantum phenomena (micro micro physics) were discovered, their incredible similarity with unitary vector spaces (algebras of vectors and operators of unit norm, unit intensity) was noticed. Quantum mechanics then became the story of linear algebra when it was confirmed that interpretations of these vectors and operators happen in experiments, and this happened without exception and with accuracy never seen before in physics.
Question: What is interpreted with what?
Answer: Vectors are representations of quantum states (particles, or waves), and linear operators (their interpretations are also matrices) are representations of quantum processes, the so-called quantum evolution. The A process acting on the x state translates it into a new Ax state. Repeating the experiments, we identify the process and the state as a matrix and a vector of unit norms) and continue with the calculation.
The beauty of that story is in the simplicity of linear algebra (of course, for connoisseurs) and experimental confirmations of the calculated, with extremely high certainty. Accident is the difficulty of interpreting the results of computing, understanding, and devising appropriate experiments.
Question: Where is the "information theory"?
Answer: The x state is static, as is the A state. Acting with A on x a new state Ax appears, a new vector, and the jump x --> Ax is discreet, discontinuous, there is no sure way to find out what happened "in the meantime". This discontinuity is a specificity of "information theory" (mine) in the otherwise now classical quantum mechanics. Repeated "news" is no longer news, so now these transitions, the mappings themselves, are becoming the main places of events.
Question: How do the sums of "perception information" appear here?
Answer: So S = Ax + By is again a quantum state, that is, a quantum process. Literally both, because linear operators are also some vectors. Those with the vectors they act on make the so-called dual vector spaces, and these are gaining in importance in "information theory".
In order for S to be what it needs to be, additional conditions are needed for states (x, y) and processes (A, B). Hence some other features of the quantum world, such as Born's rule of probability, or, for example, the division of elementary particles into fermions and bosons.
In general, certain processes can only take place over certain states, but conversely, given states can only develop under appropriate processes. Thus, we further understand the "duality" of state and process. Unitarity (normality per unit) means the reversibility of these processes, and it in turn leads to the law of conservation (both the states themselves and the processes).
Correlation
Question: What is important in the information model of the world that distinguishes it from the classical materialist model?
Answer: Communication, interaction. Living, or inanimate beings, phenomena, physical states, bodies, or particles, let's call it what we want, in pairs are more or less correlated. Their mutual relationship expresses information of perception, S = ax + by + cz + ..., an important quantity in information theory, and insignificant or unnoticed in the classical materialist concept.
What cannot communicate with the environment does not exist for a given environment, but vice versa, an environment that cannot communicate with a given subject does not exist for a given subject. This phenomenon (if it does not communicate, it does not exist) has been observed in physics for a long time, but it is there as a foreign body, something without which science "equally well" functions. However, in information theory, this mutual relationship of the two entities is the starting point of everything.
For example, in a given sequence of events, say, the "abilities" of the subject participate with the values a, b, c, ..., while x, y, z, ... through the corresponding values of the "resistance" of the object. The sum S, the sum of the products of the pairs of these sequences is a measure of their presence in reality, the vitality of a given "conflict" situation, i.e. information.
For example, in the book “Information of Perception” (p. 88.) a well-known example of the correlation between air temperature and ice cream sales is cited. The higher the air temperature, the better the ice cream sales. Because similar correlations are now "the essence of the world", that is why this "information model" is so strange, new and repulsive. But thanks to its greater universality and equal accuracy, despite its strangeness, I believe that it will prevail in some future science.
Think how repulsive it was at the time (end of the 19th century) Boltzmann's the concept of molecules in explaining heat energy, that is Mach, the leading philosopher and physicist of the time, stood up at one of his presentations, turned to the audience and exclaimed: "People, this man is a fool, molecules do not exist!" Boltzmann soon killed himself, and only a few years later the molecules were accepted in physics. Moreover, today we do not consider a "scientifically explained" phenomenon in chemistry, as well as in biology or medicine, one that is not explained by molecules.
Representative
Question: Why do you only take a representative in the distribution and not other outcomes? (Questions are related to my book “Physical Information”.)

Answer: An even better question would be why is a representative sufficient for the conservation law to apply to the information? I don't know the best interpretation, but the evidence is there that such formulas work. As far as I know, they are the only representatives of "information conservation". Let me remind you, Shannon's formula (1948), like the others known today, does not define the information for which such a law would apply, the law of conservation.
Question: Still, maybe there is some explanation?
Answer: Yes, I have them. One is about news that is no longer news when it happens again. The second is "appearance", , the emergence of more intelligent behavior, say masses of ants in action, from their non-intelligent individuals.
In the above book, I deliberately avoided such interpretations so as not to dilute the sharpness of the theorems, which are quite new there. These interpretations will be the subject of new attempts to understand information, more or less successful speculations, small steps or those without which new (hypo) theses cannot be major strides in science.
Question: Do you sound distrustful?
Answer: If so then that is good. The job of a scientist and someone in general who would search for the truth is not to believe, but to doubt and check. The falconry of today's science is too much reliance on authorities, on profit and sponsors from magazines to institutions. All that alienates science, and without that, science seems impossible. Authorities have their own interests and make compromises with research, so they easily become guardians of dogmas and start avoiding suspects.
Interaction
Question: How do you think the normal world will understand that reality is in the interaction of "subjective" and "objective", and not in the entities that interact?
Answer: Not at all, and I don't worry much about that. I think that is easy to explain and that whoever wants to understand will understand. But if the "theory" is difficult to understand, then it is better to ignore it until further notice and forget it.
For example, the energy of E "subject" (bodies, particles, waves) is ascertained by means of "object" (observer, relative coordinate system, measuring apparatus). We only imagine that the "normal" state of the measured is some Eo energy of rest, and in fact there is no such thing in a world that is constantly moving and changing. Depending on the observer, the E values are always different and different from the Eo, which is again just one physically special case among the observers.
So, it is in quantum mechanics. There (we imagine that) we have a quantum state (of one or more particles) which we call a superposition, and here it can also be a "subject", a sequence (a, b, c, ...) that defines the probabilities of the outcome in appropriate situations, which is also a series (x, y, z, ...) defined by the measuring apparatus, which we can also call an "object". In this case, what we get, S = ax + by + cz + ..., is the result of measurement, which in (my) theory of information we call "information of perception". For simplicity, for an "object" in physical measurement, it is usually assumed that only one of the coordinates is different from zero.
We know nothing about the very first sequence, nor about the second, until we put them into interaction, conjugation. This is the essence of "information theory", to admit that we know nothing about the possible "reality" in itself, but only something about the one we "catch" by communication, the sum S. Such an understanding used to be the domain of mere philosophy, which is only now channeled with concrete formulas, and the results of those formulas "work".
Creativity
Creatives are messier, because both they and the tidy intuitively feel that excess options are the opposite of order. Of course, none of the options in creativity without abilities, so we have so many more "messy" than "genius". On the other hand, concentrating on a small number of options, having power and teamwork, and even worshiping authority, also have their advantages. One is certainly the satisfaction of natural aspiration, giving up life and approaching death, from greater to lesser vitality.

The deeper cause of these instincts is the principled minimalism of information, but you still won't find anything about it in public science, not even in this article. (Messy People). Still, it is interesting to read it, if for no other reason then because of at least a little better understanding of tomorrow's science.
Liberty
Freedom belongs to the category of phenomena related to the amount of options, information, vitality, scope or capacity of action, initiative, risks, aggression, combativeness. Everything opposite from relaxation, death, sluggishness, passivity. I mean, the problem with life is that its essence is freedom, and you have to conquer it. Freedom comes with tension (life) and contrast calms it (death).
Inflexion
Question: Is there anything interesting that you haven’t written or told about equality at all?
Answer: Of course, but let it be known that whatever is important to say now, I will retell and leave it somewhere in public. Let's start “Notes I”, in the title “26. Gravitation Multiplicity” and especially the subtitle “Space curvature”, on page 102.
We know that Gauss discovered a method for defining the curvature of a surface (Theorema Egregium, 1827) which cannot be removed by deployment, it remains invariant. Because of it, cartographs from the globe cannot be accurately transferred to the plane. His student Riemann developed the idea of that discovery and found the "Riemann curvature tensor", which contributed to the popularity of the tensor calculus (among mathematicians). Einstein (1916) then applied this theory to his General Equations of Relativity.
Geometry was the historical beginning of many branches of mathematics, and if not then at least inspiration. Gauss's idea took me hours in modeling the wave nature of matter, cyclic movements that preserve information, the impossibility of (absolute) homogeneity of physical structures and, here we are, equality.
Question: Do you mean social inequalities here?
Answer: That's right. For example, in the Roman imperial method of "divide and rule", which actually relies on the natural tendency towards particularity. When you start to shape the geometric model of a sphere, with a drawn structure, into the surface of another Gaussian curve — it deforms. Whatever force (excessive information) you use in society, society changes its "curve" and "shoots at the seams." It is a development that certainly happens, because there is no part of this world without information, and every amount of it (surplus or deficit) in a certain situation becomes "excessive".
One day I may give formulas with drawings that I worked on this topic, but for now only this. See also my recent previous answer Equality which concerns the same issue.
Question: Can I have a detail, I won't tell anyone?
Answer: Neither say nor refine and publish under your own name, ok. Notice that information perception (S = ax + by + cz + ...) has the form of a metric of space (ds2 = gij dxi dxj, where according to Einstein's convention it is added by repeated indices). Metric tensor coefficients (gij) define the curvature of space, which according to Gauss's theorem (1827) is the invariant of space.
Riemann curvature tensor (Rijkl), defined by the coefficients of the metric tensor, it is invariant, it cannot change without changing the energy of the field itself, without degenerating the previous curves and without changing the forces. I hope it’s an analogy (S) with the geometry of physical space-time (ds2) now obvious.
Question: What does insisting on equality lead to?
Answer: That is a good and difficult question.
Equally probable outcomes are more informative, and nature tends to emit less information, so it turns out that it does not like equality. The consequence is also the need for force and the consumption of additional energy, in order to move towards equalization.
A more informative system is more vital but also more expensive. Therefore, in the conditions of equality that we are building today with legal systems, we have better opportunities for greater development, but also a larger number of lawyers and administration. In an even greater insistence, I suppose, some now hidden models of information avoidance could work in society, for example analogous to stronger gravity where "excess information" escapes into a parallel reality causing a "space-time curvature".
Remember that the "world of information" is actually a world of multiplicity that can almost always surprise us. Therefore, the story of the details of the mentioned models of avoiding redundant information should be imprecise, especially now in such an early period of theory.
King
Question: How do you mean to "explain" that freedom should be fought for and that it does not come as a gift, isn't that clearer than an explanation?

Answer: The slogan “Freedom is never voluntarily given by the oppressor; it must be demanded by the oppressed!”(Martin Luther King) is battle call, but in a special way also the truth that can be derived from the principles of "information theory".
Namely, from the claim that "freedom" is the amount of options, or the amount of uncertainty, and therefore information, it follows that the laws of information apply to it. One of them is that the more probable outcome is less informative (the news "the man bit the dog" is bigger than the news "the dog bit the man", because the first one is less probable). The consequence is that events develop towards more probable, i.e. less informative ones.
So, the development of events spontaneously goes towards less information, i.e. less freedom, and therefore the move towards greater freedom must be spontaneous, violent.
Science sometimes proves the obvious, not so much to check the obviousness itself as to check its settings. For example, we find this in the teaching of the basics of geometry to the astonishment of students, when we derive strong proofs of otherwise known attitudes from the axioms of geometry.
Barbarians
An exact theory cannot be in contradiction with oneself, or with another correct theory, or with any practice. Therefore, to each question, if there is an answer, it must agree with the "information theory", or I will have proof that part of that theory, in relation to the context, is not correct. This is how my guess works in the end; I test the theory in the most incredible conditions possible. That is the answer to the first question.
Another question was to give an example that I have not done so far. Of course I have such, we should consider them for hours.
For example, the attraction of civilization to barbarians — is a broader concept. When a society becomes civilized, it becomes better organized, which means that it distances itself from excess information (dangerous, harmful, useless) options. A state with less information is more attractive than a state with more information, because the principle of minimalism of information applies to everyone, so there is an attraction similar to gravity, or the desire to organize in general (handing over part of one's freedoms to a wider system).
We unconsciously understand this lack as comfort.
Its appearance is a moment that significantly separates us from, say, the bee society, from the point of view of information theory. Bee society can be static (lasting almost unchanged for millions of years) because the bee has very little information of perception and little scattering. There are no separations of "barbarians" among the bees, which would then attack the "civilized", because the space for these spreads of that kind is too small. Of course, static is additionally conditioned by a constant environment.
Revolution
Question: Are after the periods of great lies in the history of civilizations follow their great changes?

Answer: Yes, probably, but you will be disappointed if you expect an answer from a historian, sociologist, psychologist or mere statistician. The closest thing to that would be to say that a lie is hard to sustain, and a big lie even harder.
Your question has an even deeper answer from the standpoint of "information theory". From what has been said, that nature likes to hide its information, i.e. actions or truth, or from its principled (universal) minimalism, as a reaction to action (Newton's law) it also follows that new uncertainty (information, action) rushes towards deficit and unpredictable changes.
Question: Can you confirm your (hypo) theses with a firmer point of view?
Answer: Yes, let's say in principle that it is more likely to happen more often, that it is less informative, so the deficit of information in the development of events is expected. An even greater deficit arises by concealing information (untruth), and then due to the same principle (minimalism) it will try to be supplemented — because some uncertainty (information) will additionally want that position.
Or, say, because work is the action of force on the road (dE = F ⋅ dr), that accumulated labor is equivalent to energy, and the product of this and time is information. In other words, in order to create a deficit (surplus) of information at a given time, work needs to be done. On the other hand, putting the truth under the rug, as well as unconscious lying, are processes that require additional use of force. That excess force (negative or positive, attractive or repulsive) threatens to explode.
In addition to these three reasons, I have more, but let's wait for the above-mentioned laws to be "discovered" by historians, sociologists, psychologists and statisticians, so we will continue.
Rock paper scissors
Question: The program works perfectly and then suddenly goes wild, why? (An extensive code was sent to me with more questions, explanations, and complaints.)
Answer: The problem is with the statistics and one similar oversight I had recently. I guess the program is otherwise "perfect", I did not go into details, but at least one catch is wrong. Not all order relations are transitive!
Namely, if 3 is greater than 2, and 2 is greater than 1, then 3 is greater than 1. This is the "transitivity" of the relation "greater than" (order). However, although "stone" defeats "scissors" (rock breaks scissors), and "scissors" defeats "paper", "paper" defeats "rock" (paper covers rock). I'm talking about the game "Rock Paper Scissors" (Rock paper scissors). Read my mentioned article now , not to repeat, so turn off "transitivity" in the program when you don't have it in "order".
Question: Wow! Great, it works! How can this occur to anyone?
Answer: In information theory, I had a similar problem (a long time ago). It follows from the principle of minimalism of information that all physical systems slowly and spontaneously pass into less informative (more probable states). However, the law of conservation information (also probability) applies, which seems to be a contradiction with the previous one!?
Another example, if the essence of information is uncertainty, then repeated "news" is not news. With a spontaneous tendency towards as little news as possible, the question arises why this world does not fall apart and disappear? If the law of conservation the amount of news applies, then the question is what keeps that news from spontaneously splitting into smaller and smaller pieces and disappearing into infinitesimal powder?
Then I noticed that mathematics has long had a solution in the form of "non-transitivity of the order relation". The idea is henceforth, but that is not all.
Karma
Question: Is there karma?

Answer: In the theory of information, "karma" would be in accordance with the two principles of information, minimalism and conservation, and in contrast to the uncertainty which of these two is even the older essence of information (from this third we derive too two). So, setting karma as a principle, or legality, would make information theory imprecise, nebulous.
By the way, karma (pali: karma - act, deed) is a term of Indian philosophy which means the relentless and inevitable maturation of each of our wills or deeds, that is, every action that starts the chain of causes and consequences. Karma keeps man in the eternal course of events, which is considered a source of suffering and from which liberation is sought.
Therefore, according to the original meaning of the word, karma is a physical action and it is the equivalent of information. However, according to further interpretation, karma is causality, so in that sense it is the opposite of chance. According to even further, karma remains only in the domain of emotions. So, we see how complicated the "information theory" is (as well as the truth when we go into details) and on the other hand general and simple, that is, how naive the ancient understanding of karma was from the point of view of modern analysis.
Question: Can you give an example?
Answer: Can. Imagine an injustice done to someone. Let's say that the overpaid bill at the cash register was missed by a customer who later noticed that "lie" and understood it as a fraud, and then slandered the store.
In jargon, we say "the world is small", which is actually the expression "six-step rule" according to which in the case of "free networks", in the worst case, one gets from one to any other node. I'm talking about a network of equal links, the form of which is often followed by the acquaintances we make, which is why it happens that the malice of a deceived customer comes back as a pity to the store. Otherwise, and especially when an unintentional return echo hits the "deceiver", we say that karma, an evil fate, has reached him.
Such mistakes can also be accidental, that the seller made a mistake, appeared on some occasion, apologized, and even compensated the damage, when the alleged karma can be returned to the buyer due to defamation. This can happen, for example, in the form of a loss of trust by an acquaintance of the allegedly injured person, who would now be seen as a slanderer and a liar. Then the "gossip" could successfully explain that he was in confusion and shift the karma to those who hastily and unjustly doubted him. And again, similarly. It is clear that such injustices, individual or in waves, are the consequences of some laws of nature. Not knowing them, or simply wanting to simplify things, we call them karma.
Question: Okay, so where's the "information theory"?
Answer: That’s a good question and luckily, I have one likely answer. First of all, a lie is a hidden truth! Any information, event and anything in general that could be proven to be impossible — cannot exist. Thus, in the theory of information, we interpret the "untruth" of the algebra of logic as a "lack of truth". From the standpoint of the principled minimalism of communication, according to which nature is more prone to greater probability, or less uncertainty, we appropriately say that a lie is "hidden information". One way or another, this deficit occurs in situations of deception, masking manipulation, suffering (a living being has an excess of information in relation to the sum of dead matter of which it consists), or in general in turning active information into potential or its actual reduction.
Thus, fraud creates a need for uncertainty (information, amount of options) due to the principle of minimalism. It is not possible to predict exactly what is triggered by this, the increase of "good" or "evil" for the fraudster, but only speculation, fear that "evil fate" is more probable, or hope that failure opens space for new sudden success.
Feminization
Question: What is "feminization" in information theory?
Answer: It is an expression that somehow stuck to the interpretation of one aspect of my generalization (thermodynamic) entropy, while I was trying to convince a couple of colleagues of the idea. Like the "spin" of a photon, or the "color" of a quark, it does not correspond to the best essence, but the thing is so new that there is no appropriate expression in any language in the world and the name has remained. Read the popular introduction "1.4 Feminization" in my book „Physical Information“ attached, not to repeat, because there is more.
The physical system can be more turned to uncertainty (communication) outside, or inside. When this is the second case, then it is "feminized." Then there is a more intensive "organization" of the interior than of the exterior. Such a system becomes more orderly on the inside, but more vulnerable on the outside. This may be clear from the aforementioned introduction, but many of the observations that follow from it are probably not.
For example, in the mathematical theory of games, "competition" is a situation in which we strive for "victory". Unpredictability is an important moment in the competition (the more interesting the competitions are for information theory), and one of the most successful tactics is “Tit-for-tat” then the subject (competitor) must be more turned to the object (opponent) than to himself, so the "feminized" situation is the one that leads him to defeat.
Question: An eye for an eye is not a new tactic, why do you consider it new?
Answer: Yes, the answer is to the first question. We recognize the tit-for-tat tactic (close to ours nicely for dearly, or eye for an eye) in various forms throughout the animal world. Evolution has filtered us out that we mostly react to ignoring by ignoring, or to fear by fear, because so we have had a better chance of adapting or surviving. It is also recognized by the histories of civilizations, where the most successful warriors treat the aggressive peoples without pardon, and friendly to those who favor them.
However, only recently, after computer simulations, has mathematical game theory recognized the values of tit-for-tat tactics. In textbooks written until a couple of decades ago, you will find an overemphasized accent on its flaws, for example in the case of the "prisoner's dilemma", which otherwise works better among criminals than honest people.
Its otherwise popular challenge is Gandhi's famous remark that applying the "eye for an eye" tactic, the whole world would quickly be left without eyes is questionable. On the contrary, simulations show that then more often, or more easily, there is a balance of power, that is, a sudden but stable compromise. We want the strong for the allies, and we subdue the weak.
Question: Do you seem to underestimate cooperation and compromise, them as a basis for stability and progress?
Answer: If it "seems so", then we do not understand each other of how to achieve cooperation. Simple computer simulations show that the best balance (if any) is gained by competing forces. Where a compromise is established by heart, without reciprocity and letting the "conflicts" strike a balance, it is unfair. One side will feel that it is dominated by the other, that subordination has actually taken place.
Everything in nature works that way, from the situation when you pour water into a vessel which, due to the swirling of the mass, through "conflict" of particles, comes to calm with the horizontal surface of the liquid, to the fencing of hunting (feeding) of wild (free) animals in nature. Simply put, it is not true that the "eye for an eye" tactic (in the way of information theory) will lead to all people being blind in the end, but on the contrary, it is often the only thing they can do, both of them, the weaker and stronger, to make them less blind.
Question: The principle of information speaks of the general tendency of nature to more often realize more probable outcomes, that is, states with less communication, calmer, lazy, with less action. Okay, but then how do restless states come about?
Answer: Its "anomalies" are also part of that principle. Entropy grows spontaneously and we have the "Gibbs paradox" — when it does not grow. Everything would like to cool down, but some processes go faster than others, so there are disturbances that are rave and tempests. Mercury always goes around the Sun in the same direction, although we sometimes see its movement from the Earth retrograde.
Also, all particles and bodies accelerate equally downwards under the action of the earth's gravitational force, and in spite of that geysers and volcanoes happen around us. Finally, the combat tactics of reciprocity (tit-for-tat) lead to a more stable peace than a compromise written by heart. I agree that this may seem confusing, but behind "feminization" remain both calming and disturbing processes. Here are some more, I hope, unusual examples.
When individual cells tend to release excess of their own information more than the organization to which they belong, that organization becomes "more alive." Let me remind you, the law of conservation applies to information, and when it is nowhere else, it accumulates where it can. Parts of the system more prone to "feminization" tend to go in internal as well as into external organization. That sounds absurd, because feminization itself is a term here that should mean a lack of interest in external events.
A male aggressive society, like a chimpanzee, arises from an excessive need for peace in one of its parts, and this part of it from an aggressive wider environment. On the other hand, the resulting aggressive, competitive behavior of the group, in appropriate conditions, together with the tactics of reciprocity, quickly lead to wider calm, and then to a female society — like bonobo monkeys, close relatives of chimpanzees.