October 2021 (Original ≽)

Figuration

Question: What is the problem with the "shape" of the elementary particles of physics? I noticed that you like to add "discoveries" of others articles to your texts that talk about the forms of the smallest particles of the substance, but never use them further ...

Answer: You noticed well. I keep the possibility that a particle of light (Multiplicities, Eccentric photon, p. 67) or some other has a "shape" in reserve, but I do not believe in such a thesis. More precisely, I leave them in the texts simply because others read them as well. You could understand the reasons for doubting the "shapes of the smallest" if you listen to this video (Finite Volume, Infinite Surface Area) which otherwise has little to do with our current story.

Namely, there are bodies of finite volume and infinite surfaces, and they were discovered centuries earlier. Because of the mathematical possibility, because of the abstract existence of such bodies, there are contradictions in physics that would insist on " figurations" of arbitrary parts of matter, and I do not want the "information theory" to stumble on that. The real reasons for my disbelief in the "shapes" of the smallest parts of physics, however, are on the other side. I have written about it several times before and I will repeat them briefly.

First of all, the tissue of the cosmos is information and its essence are uncertainty. Second, there is Fourier's theorem (Joseph Fourier, 1822) which says that almost any function (any physical trajectory) can be approximated accurately enough by a fragment of any other such function. This can be interpreted with the view that the smallest fragments of paths (substances) can have any shape, and then that further means that they do not actually have a shape.

Third, there are Heisenberg's relations of uncertainty, which, generalized to the principle of uncertainty, show that the impossibility of accurately determining the position and momentum (energy and moment) is deeper than our local powers of measurement. It comes from the noncommutativity of the operator — which is an algebraic phenomenon and therefore inevitable.

Area

Question: How do we know that information is two-dimensional?

Answer: Such is the nature of information of perception S = ax + by + cz + ... (book "Information of perception", 3.6 Stereometry of statistics, p. 91). It is a scalar product of two vectors, two series of observables (a,b,c,...) and (x,y,z,...), which crucify 2D space. However, the picture on the left solves Hawking's "Science of Black Holes".

Black holes are such massive astronomical bodies that their gravity also traps light. Everything they swallow disappears forever from the outside world. As is the case with information, it turns out that they eat the past of the universe; little by little it is as if they are real holes where the memories of the universe disappear. At least that's what Stephen Hawking looked like when he thought about them in the second half of the 20th century (Famous Paradox).

But the same theory of relativity that predicted the existence of black holes can save the law of conservation of information, here's how. Observed from the outside world, time flows more slowly and the radial lengths of the body that falls into the black hole shorten, so that it never actually crosses the "event horizon" (the boundary sphere beyond which there is no return), but becomes thinner and stick to the surface of the sphere as an image. All the contents of the collapsed body become 2D images on the border of the black hole event.

Therefore, what somehow looked like a celestial body, that lasted or ever happened to it, after falling into a black hole, becomes torn, crushed and ironed, but with the preserved total information in its basic form — as a surface. The loss of previous connections and the complexity of the forms they could define may indicate the possibility of different interpretations of the past, or at least its partial vagueness. But that is another story, for later in the continuation of such a conversation.

Before that, we notice that time slows down the body's decaying and entering an increasingly strong gravitational field (black holes) in proportion to the increase in its energy. At the same time, instead of virtual vacuum particles, real ones are created in the same ratio. From the point of view of an external observer, in shorter and shorter relative times (a given body needs more and more of its own, proper time), the energies of the intrusion system are increasing, but so that the product (energy) × (time) remains constant. The product (momentum) × (path) does not change in the direction of gravitational force, with a similar explanation. We are still in the theory of relativity, although it can rightly be said that we are talking about Heisenberg's relations of uncertainty.

Space and time in the theory of relativity, as well as in the theory of information, are manifestations of one and the same phenomenon. In order for light, or information in general, to reach an observer from a distant star, it takes some time to cross a certain path. It is not realistic to talk about the path without wasting time, so then every observation is an observation of the past. The past is therefore a kind of reality. To distinguish it from the present, I also call it pseudo-reality. Otherwise, the present consists of events on the paths of space-time through which light could pass.

Like light radiating from a distant star on all sides, so various information is emitted from every body. In this way, bodies communicate, both with each other and with space. Observing from an increasing distance (d_a) a given path (a) that light (information) passes vertically (a ⊥ d_a) to the direction of observation, the product (a ⋅ d_a) is constant. Half of that product represents the area of a triangle whose base is the distance traveled and in the third vertex is the observer. This area again represents all the information that was emitted from the past (base) to future events, all the way to the current observer. It (a) is diluted, we can say, so that the person in question sees it less and less, at an ever smaller angle, the more distant it is (the greater the d_a), but in total, considering all the layers of the past between the date and the observer, it is the same.

Information is the fabric of the cosmos, so forces are also a kind of information. That is why we have Kepler's second law and its generalization to all appropriate forces, as I discussed in the central movements in the book "Notes to Information Theory".

Chords

Question: Do you apply the alleged two-dimensionality of information somewhere?

Answer: In addition to a few articles on "central motions" in the aforementioned book "Notes I", where it is proved that movement on conics (ellipses, parabolas, hyperbolas) is caused by any central force only if its action spreads at the speed of light, I can reveal another interesting an application I did not mention there. Notice the following figure on the right.

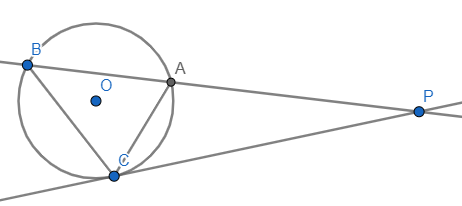
From point P, the line that intersects the circle of center O at points A and B and the line that tangent the circle at point C are drawn. From the peripheral point A, the BC chord is seen at the same (sharp) angle that the tangent makes with that chord. Hence, the triangles PAC and PBC are similar, because besides the common angle at the vertex P, they have equal and (obtuse) angles at the vertices A and C. Therefore, PA : PC = PC : PB, and hence by cross multiplication

PA × PB = PC² .

In other words, the product of the lengths PA and PB is constant, as long as the position of the point P with respect to a given circle with center O is constant. This is another, also known theorem on circles.

When we flatten a circle with respect to a given outer point, like an ellipse whose shorter half-axis b would then go in the P direction, as opposed to the longer half-axis a which would be perpendicular to that direction (a ⊥ OP), the product of these segments (PA and PB) would increase. Analogous to the information of perception, and also to the surface area that represents the information, which moves the body from whose constancy of the Kepler's second law follows, the principled minimalism of information will return the flattening of the ellipse to the original circle. It is a model similar to Heisenberg's uncertainty relations where the product of the uncertainty of momentum and position of a particle, or energy and time, forms a "rectangle" of constant area, otherwise of the order of Planck's constant and physical dimension of action.

Question: Where do you see the application of this geometry in the microworld, for example?

Answer: A particle-wave of light (photon) transmits information in the direction of its movement. It is an oscillation and in that (figurative) sense represents a periodic circular motion. The shortening of its wavelength (Greek λ — lambda) is inversely proportional to its momentum (p = h/λ), and also to the energy (E = hc/λ). The excess information that would be created by "flattening" (shortening the lambda) is compensated by increasing the momentum, and then the energy. In particles in general (all matter is also of a wave nature), this is then manifested by an increase in amplitude, which further means an increase in the probability of its finding in a given measurement (Quantum Mechanics, 1.1.6 Born rule, p. 59).

Invariance

Question: Perception information depends on the subject and object of perception, you say. But what about its relativity from the point of view of third observers?

Answer: There is no such, mostly. This seems incredible at first glance and that is why I have calculated this absurdity so carefully, among other things, through the "Variant Vectors" from p. 77, in the book "Notes II". It is shown that by changing the way of movement, the relative position of the "third observer", i.e. coordinate system, the components of the subject (a, b, c, ...) change, and then in a special way the components of the object (x, y, z, ...), but so that their "variant product" S = ax + by + cz + ... remains unchanged. The obtained product, of the covariant and contravariant vectors, is information perception.

The finding of a kind of objectivity of "information perception", its independence from "third observers", in the theory of information came to me later, almost as a surprise (because the subject itself as well as the object is relative), but more broadly it is not an unknown phenomenon to theoretical physics. I remind you that in this way, Einstein, starting from the invariance for gravitational fields and the assumption that the "geometry of space" is equivalent to the "energy of space", derived his general equations of relativity.

Because of these "strange" starting points, his equations were not well understood and were initially considered nebulous, roughly painting on something where details were needed, until the accuracy of their solutions (now beyond ten tenths of a meter, second and kilogram) in measurements was noticed. Therefore, gravity is unavoidable by possible translations, rotations or similar changes of third observers.

Dogma

Question: Tell me something about the power of persuasion?

Answer: A dose of lies makes the information more attractive (World of Lies), and then when anyone's beliefs become "their own" then it's harder to give them up. This is a short explanation of the famous saying "it is easier to fool people than it is to convince them that they have been fooled". By the way, the well-known sayings are generally not true when viewed more broadly, again because of the same thing — that a dose of lies makes information more attractive. The deeper cause of this is the principled minimalism of information. Information is higher if it announces a less likely event, and more likely outcomes are more common.

In other words, the principled maximalism of probability is equivalent to the principled minimalism of information. And as the first is the universal law of the cosmos, so is the second. That’s why it’s easier to encode than to decode, that’s why a lie is easier to spread to the media, fiction is more fun than proving theorems. Because of the same, we do not like too much freedom, unnecessary risks (they have more options, they are more informative), great aggression, actions, so we strive for less communication, less interaction, we are more inert. Also, from this principle arises our need to exchange surplus options and, therefore, freedom, for more security, efficiency, money (working for the employer, sacrificing our free time) and to submit to someone in general (Domination), but also superior (power and rule also limit the powerful or the ruler).

The principled minimalism of information, barely noticeable but persistent, leads us to prefer routines to originality. It is the general driver of our need to seek natural and social laws, standards, to standardize and behave according to protocols, legally, according to customs, that is, to be "normal". That is why every civilization at its zenith will strive for legislation, more in the future than in its past, going then (unconsciously) to over-regulation and into decline of its vitality. She then begins to die in the informatic sense. It is governed again by the same principled inclination which makes us more attached to half-truths, dogmas, than to truth.

Equilibrium

Question: What could be wrong with a stable, well-balanced economy, legal system and society in general?

Answer: First of all, obsolescence. Equilibrium in physics is a state of the system where its total energy does not change over time, which due to the principle of least action means that it is then at the local minimum. It takes a big jump over higher values to possibly achieve some new lower (local) minimum energy, and when the system does not have the power to do so, it remains trapped in equilibrium. Not all minima are the same.

In the picture from the left we see a stable, unstable and neutral balance. It is similar in the economy, or with social stability. Then, instead of energy, we can also talk about information, because unlike inanimate beings, these "quantities of options" (information, actions) have enough in excess that their reductions can be counted on. The principle of the least action of physics is actually a consequence of the broader principle of the least communication, the principle of minimalism of information emission. Similar to capturing inanimate matter in a state of lower energy, or less communication, so life can be equally slowed down and blocked, spontaneously striving for lower values.

Like the energy of a pendulum, which is slowly expended by friction in swinging while its oscillations decrease going to a state of rest vertical below the support, because the excess energy cannot just be handed over to an environment that is all made of energy and would also dissipate itself, are also difficulties with the desired release from freedom. By reducing options, we focus, become more efficient, safer, or calmer, but the path to that more optimal state (less risk, less need for vitality) can be easier than the other way around, from the path to originality, uncertainty and fear of freedom. Especially if we have already fallen into a deep state of balance, which in the case of a living being is the absence of vitality, close to death.

The lowest states of information, as well as energies, exist because actions are quantized (Reaction to Action), and they can be maintained because there are nontransitive order relations (Cycles). Similar local minimums of free market information (capitalist economies) are noticeable in developmental stagnation that is overcome by leaps and bounds (transitions of quantity into quality, Physical Information, 1.6 Equality, p. 13), but they do not have to happen in too rigid environments and then there are paths of decline. That is why a society with efficiency that lasts is necessarily dictatorial. The bad thing about such people is that they become obsolete and lag behind over time.

Yin-Yang

Question: What is the "unity of opposites" according to information theory?

Answer: The unity of opposites, or yin-yang, is a consequence of the news which repeated is no longer news, the law of conservation of information and the assumed structure of the cosmos that consists of the information itself. It is thus recognized in "information theory" (mine).

From them follow repetitive structures, not only in the wave nature of matter in general, in repetitions of climate change or historical events, but also in different evolutions of vision into the same eye morphology, and even in mathematical patterns (e.g. addition tables) that we can apply in seemingly incompatible situations.

Hence, in the best, say stable, well-balanced economy, as well as in a similar legal system and society in general, we can find flaws. One such negativity explained without the need to mention yin-yang is mentioned in the previous text (Equilibrium).

Misinformation

Question: Excess information hurts a good decision?

Answer: Yes, as well as shortage. Here is a description of exactly that (Internet addiction) which concerns excessive search and the Internet. But this is not just a problem of "our civilization", nor a problem of people in general, of our own kind, but a matter of principle of the overall nature of information. Information is the fabric of the cosmos (space, time and matter), its essence is uncertainty, and it is ruled by, say, two principles: minimalism and conservation.

The principled minimalism of information is equivalent to the spontaneous more frequent occurrence of more probable outcomes (they are less informative), and the law of conservation of information is also from the same of the probability. This second reason (about the law of conservation of probability) is less known, perhaps unknown, and only seemingly less relevant to the question. Because of it, the glass on the table from one moment will be in the same place and in the next moment, until some body (the hand that moves it) or some force acts on the glass.

Well, the nature is full of information, but it's as if she doesn't like it, because she would like to have as little information as possible. We can state this in different ways, and the ways are again hers (sometimes known to us, sometimes unknown, and sometimes unpredictable) to extract information from surplus in a less informative way. One of them is that with too much information we become misinformed, similar to when with their lack we remain uninformed.

Question: Do you have another example of turning excess information into a lack of it?

Answer: In addition to the Pseudo-reality into which the excess matter escapes, and about which I wrote more often, there is also the so-called "The transition from quantity to quality" and a special discovery that Quantum computers could be better than the sum of their parts. I have earlier contributions on Quantum calculus, and the answer to this question would be an appendix to them. From the breadth of these two examples, you can see how extensive the "principle of information" is, not to mention further.

Contras

Question: What do you think about the people who are constantly against?

Answer: Having your own opinion is not always the opposite. It’s too simple for reality, but while just as stupid as always agreeing, it can be a good introduction to understanding the complexities of this world.

The world of lies (Dualism of lies) is equivalent to the world of truths, but lies are hidden truths and it takes a little more effort, the ability to decipher. Stupid people also understand the truth. With the help of lies and tricks, hunters hunt game, ruling by manipulations and cunning, generals win the war, managers conquer the market, and politicians the masses. Understanding lies and mastering them is a higher form of intelligence than simply listening to the truth.

However, what happens, what we call physical reality, cannot be events that we could prove cannot happen. That is why I say that every information, as well as every physical action, is a kind of truth. There are no real "lies", it never happens, a lie is like a "yes-no electricity" in electric gates, a substitute for "higher-lower voltage". In addition, based on principled minimalism (action, communication), half-truth is more probable than pure truth.

If it were not so, this would be a world of pure truths, lying would be impossible, and to agree would mean to be on the only right path. There would be no other options and we would really live in a single deterministic cosmos, as the vast majority of us still believe today.

Maturation

Question: So then, is the development good or bad?

Answer: The development is, like much in a world of information, periodic, good and bad and vice versa, and that is especially true for living beings. They initially conquer new worlds (children growing into adults), so they still mature, obsolete and die. The theory information that same process also recognizes in organizations of living beings.

Maturation is actually noticing some regularities around and adopting them, or being subordinate to them, turning mostly to the internal organization and avoiding external trouble. However, the disclaimer is the loss of freedom, information and action. It is a reduction of living into an inanimate substance, because this first separates from another by amount of options — of which we want to give up unconsciously guided by the principle of minimalism information.

The appearance of a particular living being, or organization of such, maturing and outdated, the theory of information sees similar to the storm, earthquake, or geyser, that consists of the same particles for which the principle of the least action of physics is valid, or attractive gravitational force of earth, but they still arise and disappear.

Periodicity

Question: Does the theory of the information periodic phenomenon recognize?

Answer: Yes, with a limit that there are no two such identical events that would be exactly equal together with its wider environments. The meaning of local periodicities can be understood by the definition and graph of the next simple mapping. Notice how function f the numbers 1, 2, 3 and 4 of the domain maps into numbers 4, 3, 2 and 1 of range (codomain) respectively. It works for both sides unambiguous, it is bijection, which means that it has an inverse function of f^-1. Moreover, the function in the picture is inverting itself f²(x) = f o f(x) = f(f(x)) = x.

Locally periodic processes should be repeatable, that it seems to us that changes that make up the memory in a way that the image can be reconstructed from the reproduction, i.e. that copies that they make "remember" the originals. This further means that for the entity whose evolution the functions describes, the law of conservation is valid (Nether theorem). The function describing the periodic phenomenon, in the mapping compositions, from domain to codomain and into a new codomain, eventually must achieve the initial value. The complete starting domain must appear in some step of repeated mappings — as some of the copies. This is exactly the property of unitary operators whose representations are the processes of quantum mechanics.

In the theory of information, periodicity is compromising the law of conservation information and the properties of the news that it repeated is no longer news, i.e. the principle of minimalism information. I have previously explained how possible it is (e.g. Chasing tail), since each system has been strolled to reduce information, so there is no need to repeat it now.

Question: What processes are periodic?

Answer: Everyone, locally. Given the previous picture, the process that can be represented by bijection (mutually unique mapping) and for which the domain is a finite set — is periodic. In information theory both conditions are met, the first because of the law of conservation, and the second because of the final divisibility. Free information (transmitted by quanta of physical action) is always a periodic phenomenon and vice versa, all periodic phenomena are some (free) information.

Namely, if the domain (bijections) has only two elements, they must be mapped into the corresponding (same) two, in the same or reverse order. If the order is the same, that's it, f: (1,2) → (1,2), the function is constant and we say its period is zero. If we change the order of the codomain elements, f: (1,2) → (2,1), the only possible one is reversed, then the initial arrangement is created by repeated mapping with the period of the function of one step.

A bijection with three domain elements can be an identical mapping of the zero period, with one pair of permuted elements (1,2,3) → (2,1,3) of period one, or of period two in the case of shear (1,2,3) → (2,3,1). In general, bijection with n elements by the interference domains of the periodicity is always periodic. Because information transfers can be described by such functions, they are also periodic.

Question: What about chaos theory? If you claim that all physical phenomena of information theory are periodic, are chaotic phenomena also periodic?

Answer: Yes, if you mean the deterministic chaos theory of the American mathematician and meteorologist Edward Lorenz. The hallmark of his theory is the "Butterfly Effect", according to which " Butterfly’s Wings in Brazil Set Off a Tornado in Texas", which is represented by a graph of a butterfly-like periodic function.

Some "chaotic phenomena" of his theory have already been proven to be periodic, and based on them, much better meteorological predictions are made today than before. But there are also periodic ones, I claim, for which it has not been proven yet. Moreover, all phenomena are periodic, not only his theory which implies "deterministic chaos" of natural phenomena, but also all phenomena (which we can perceive with the senses) of my "information theory" that presupposes objective coincidence.

Forces

Question: Are you trying to explain physical forces with information theory?

Answer: Yes, but I'm also waiting for physics to discover something more. An important feature of "information world" is multiplicity, and even more important is unpredictability. Because of the first, the world is more complicated than it seems, and because of the second, it is in constant motion. It follows that the tissue of the cosmos is information.

We communicate because we constantly need something, because repeated "news" is no longer news, as soon as are "outdated" the uncertainty and information cease, but then comes the law of conservation and bridging the gap. Therefore, it makes sense to talk about one "principle of information", which has three aspects: principled minimalism, the law of conservation and uncertainty as the essence of information.

To all this comes the "unexpected" conclusion that the ontological material of physical reality must be information, because it would almost all disappear from this world if it could be hidden somewhere. In that story, there is a (hypo) thesis that known and unknown forces can be equivalently explained with the help of excess / lack of information.

Question: Are you talking about gravitational pull?

Answer: Roughly speaking, it arises due to the lack of information in the environment of a massive body which, due to the density of information, goes partly into a parallel reality. I am mainly talking about gravity, but I also assume some (far future) unification of the known fundamental forces of physics (gravitational, electromagnetic, nuclear weak and strong).

Question: Where are the gravitational waves?

Answer: Space-time waves, comparable to water, are created by the loss of information in a given place (cessation of uncertainty), which therefore becomes attractive (information minimalism). Cyclical processes of disappearance and filling come with layers of time and spread through space, disturbances that are at their deepest basis longitudinal like sound, rather than transversal (lateral) like a wave on the surface of water, or we believe light.

These ripples spread as the emission of information from the direction of a stronger gravitational field, if there is greater information of perception (Tension). But there are also places with a slower flow of time, so they convey that message, that time is slowing down towards the center of the gravitational field. This again means a lack of events there, that is, the attraction of substances. It is paradoxical, but in this way the stronger gravitational field, with the substance all the more in the "parallel reality", emits gravitational waves that send information to others that it is attractive.

Power

Question: What is the force of probability?

Answer: No matter how "stupid" it may seem, it could be one of the interesting questions of the physics of the future. It is already current in information theory, in this one with the information which is the weaving of the cosmos and whose essence is uncertainty, and that is why I have dealt with it before.

First of all, the development and changes of everything around us are inevitable consequences of the "information theory", so much so that even the natural laws themselves cannot escape from them. That is why the mentioned "measure of force" of probability cannot be set universally, because uncertainty is a more permanent phenomenon than force.

It follows from the principled minimalism of information, that nature spontaneously tends to less information. In order not to be annoying by repeating (e.g. that it is dual to the principled maximalism of probability — because more probable events are more likely), let's consider it through "information of perception", say a special case S = -x log x - (1-x)log(1-x), where x = p is the probability that a given event will occur, and 1-x = q is the probability that such an event will not occur. The derivative dS/dx = log(q/p) speaks of a negative change when q < p, which means that in the case of more probable outcomes, the perception information is declining.

Another important observation about the "power of information" is about the passage of time. The rate of time flow increases with the number (amount) of observed outcomes. Whether we measure the elapsed time with atomic events or home clocks, it is inseparable from (the quantity of) the outcome of physical processes, and those from the uncertainty (changes) that generate them. Therefore, time is a measure of (relative) information and vice versa. Therefore, where time passes more slowly, we will find (observe) systems of less information.

Hence the (in my previous texts) calculation of the "force of information" by means of gravity, i.e. inertia. Places where time flows more slowly are gravitationally attractive, and the "force of attraction" increases with the "voltage" of probability.

We would have to move on to the tensor calculus, but we will not do that here, because if you know it, you will search for that part yourself, and in opposite case, it is not worth interpreting it if you do not know it. By the way, you can also read this easier part (Action) about greater force in the case of (in general) greater information of perception.

Question: What do you mean by "changes of everything around us"?

Answer: The novelty of information theory is that "changes" include laws. The laws of nature change much more slowly than, say, the changes of water in the river flow that Heraclitus of Ephesus spoke about (πάντα ῥεῖ, Ἡράκλειτος ὁ Ἐφέσιος 535-475), much slower. And they also have their particular layers and their own particle-like durations.

Waves

Question: All matter is both wave and informational in nature, said, including the very laws of nature, and even mathematical statements. And then what would be the alleged periodicity in the laws?

Answer: Five is not seven. It is not true that this sentence is incorrect. It is not true that the last sentence is incorrect. Adding one such negation to each last statement, we get a longer sentence with more and more added negations. Does this remind you of periodicity? Recursions are types of periodicity as well as attractors of deterministic chaos theory (Space-Time, 1.1.5 The universe and chaos, p. 19-24).

Another example is the layering of truths given by their masking. A lie is a hidden truth (Dualism of lies). It can be conditionally said that untruth is the lack of truth, but only if secrecy is implied, not lack. The real shortcoming would be if not every higher intelligence would be able to reveal the truth hidden in the lies, and we can also mean the possible levels of development of intelligence on Earth, for example by Darwin's evolution.

The third examples are in the mentioned limitations of truth at a given place and moment. Particles, all kinds of physical events (space-time), quantum states (sets of particles), atoms, molecules and physical bodies — are also wavelike in nature. They exist locally even when they act globally (like a star that gravitationally attracts planets around it, pulls them through the galaxy, or simply illuminates them). All these phenomena are repeated again and again in the familiar environments that define them.

However, not everything in mathematics is so banal, trivial periodically. For example, the decimal notation of an irrational number is non-periodic (Multiplicities, Differences, p. 11-14). Such examples confirm the limitations of perceptions in general, but also the addition of inaccessible worlds. They are implied by Gödel's theorem of impossibility (the truth about all truths is not possible), and without them my information theory would lose an important logical basis.

Question: Are non-periodic decimal records of irrational numbers?

Answer: The explanation is an almost elementary thing that can be in the teaching of high school mathematics. For example, the number x = 45,6121212 ... has two decimal digits "12" which are periodically repeated below. Put x = (456,1121212...)/10 = (456 + y)/10, then the equation y = 0,121212... multiply by a hundred. If the period is three digits long, we would multiply this equation by a thousand, if it were four digits long we would multiply it by 10000, and so on. So, 100y = 12 + y, and hence y = 12/99 = 4/33, which means that y is a fraction, i.e. rational number, and also x is a fraction, because the sum of fractions is a fraction.

As there are non-periodic decimal notations, for example digits generated as random numbers, there are irrational numbers (which cannot be written as fractions). The ancient Greeks (Pythagoreans) proved that such is a root of the number two (diagonal of a unit square), and many others were discovered later, such as π = 3.14159..., or Euler's number e = 2.71828..., but also such is a root of any natural number which is not a complete square.

Question: How do we know that the quantities of rational and natural numbers are equal infinities, and of rational and irrational numbers are different?

Answer: This was told to us by Georg Kantor at the very end of the 19th century, otherwise the founder of set theory and the first to compare infinities with the help of bijection (mutually unambiguous mapping). But I have other methods, one of which is the periodicity of the appearance of perception. The repetition of the same or almost the same is the result of the principle of information (conservation and minimalism) and then the possibility that there are such crafts with the "poorly informed" (least information) where those "uninformed" can be like a dog chasing its tail

The phenomena that we can perceive are finite and wave. Because of the same, our "understanding" of infinity is like a "cardinal" (names for infinity), in the form of a string that can be counted, that is, which is also periodic. But this story has its "hole" in Zermel's the newer set theory (Quantum Mechanics, p. 190), where it is possible to insert another cardinal number between the countable (ℵ₀ — aleph zero) and countless infinities of irrational numbers (𝔠 — continuum). I believe that we will have to go through some cyclical understanding in spreading that idea, the Zermel's "choice theorem" from 1908.

Interaction

Question: Why do we communicate at all, why do particles interact with each other?

Answer: Because "we have to". The emission of information and communication are the consequences of "Tension", the excess uncertainty in a given situation and its resolution due to the principled minimalism of information.

On the other side, we communicate because we don't have what we need. When we are in a deficit of information in relation to the local average, to some optimum of the environment, a need arises. Then there is the resolution through communication, i.e. interaction, because "less informative is more attractive, as is more probable" (information principle).

In information theory, as we see, and explaining of the need for interactions becomes accessible, logical.

Question: Would you call it the main difference between classical information theory and the one you discover?

Answer: There are plentiful of, many of these differences, but perhaps they can be reduced to universality, more precisely to a wider range of applications of the new theory. The classical, Shannon's theory of information is mainly technically based on mathematical logic, and the new the roots accepts, and extends its basic settings to physics and other sciences (including social phenomena). It works with completely new principles in which the old settings somehow fit, but which refer to the cosmos, to the differences of living and non-living beings, society and individuals, equally to all interactions.

For example (Interaction), the source that emitted information has it in excess, and it will only go there, to such a receiver around which it is in short supply. There is no communication without this difference of tension, excess and lack, which is dictated by the "principled minimalism of information", otherwise unknown (not recognized) in classical information theory. The second example (Tension), which actually clarifies the first, speaks of the same stretch from the point of view of "information perception". The stress arises at emission and is measurable by this IP, as is the deficit at absorption.

Money

Question: How do you think the concept of money will be further developed?

Answer: If you mean bitcoin and electronic money you might be right, but I prefer to deal with predicting a much further future. From the standpoint of information theory and the principle of its minimalism, I expect a better tiedown of life and civilization of our planet in general, let's call it "feminization". It is the life path of every living being, from greater to less risk, to less of its own information or action, then from less to greater security and order.

Not to mention now that money is a "male invention" (see the answers in the previous blog), that the saying "there is no profit without risk" applies to it, which is why it will be avoided in the process of calming down (feminization). This is somehow taken for granted, and I would just add that this priority (with declining vitality) will gain value.

Also, so as not to repeat myself constantly and not be boring, here is another article that tells you a little more subtly about the same (HOW WE WORK): “We're constantly taught the recipe for getting ahead is to put our heads down and outwork everyone else. But that's not quite right...” Namely, “advancement at work” is still a “male thing”, because “jobs” are still a product of risky runs. In time, that will be less important.

Value

Question: Are you in favor of higher taxation higher income?

Answer: I would be careful about that.

Question: Have you not announced that the free market leads to the separation of fewer and fewer of those who have more and more, and that the equality of flows of money, goods and services necessarily leads to inequality in the possession of goods?

Answer: Yes. This is the certainty of the mathematical theory of free networks (Physical Information, 1.6 Equality, p. 13-14), which is confirmed by (my) information theory, in its own way. The nature of the information universe is such that it "does not like equality" and in the case of (attempts) to impose such will find "countless" ways, often unpredictable for us, to make the situation slip out of the imagined, desired equality.

Question: So what's the problem then?

Answer: With "higher taxation of higher incomes", the "house of the hungry" will be calmer, inequalities will be reduced, and that is, again, an unnatural state of affairs. What in that case "equalization of all" will not work is efficiency of the money flows. The nature of the free network forms the efficiency, as it forms the network (that rare nodes have many connections, unlike many poorer ones) to achieve better flow. It is, for example, in "six steps of connecting" between any two nodes. The danger is in the slower economic development (lagging) of a society with fairer taxation.

Question: So what do you suggest?

Answer: Give less importance to money.

Question: Won't the holders of money and power be able to prevent the "diminishing importance of money"?

Answer: That's right, it's a difficult problem for politicians who are not fighters for what they represent, but are like worms the prey of predators, or their servants.

Question: Isn't the "weakening of the power of money" the equating again with the bad consequences of the "theory of free networks"?

Answer: It is so, unless the value of money has alternatives. Some have already been good scientists, artists, parents at the expense of other values. The information world is not a paradise of equality, because it implies differences, and that is where the vent could be sought. Remember to communicate (people, physical bodies, particles) because we lack something, and we almost always lack something. Due to principled minimalism, the natural course of things will be an escape from denser information, such as a society of equal outcomes. However, the pressure is not so much from the perspective of some diluted and therefore relaxed situation of greater multiplicity (see the book Multiplicities). Beauty in particulars could be the ideal of a more just society. Courage, idea and opportunity — we concluded earlier — are recommendations for success, so decide, the theory is there, and the opportunity.

Success

Question: Working good every day is the formula for success?

Answer: Well, I don't quite agree with that. There is something in the saying that the road to hell is paved with good intentions. In addition, here we can consider more serious reasons, that the strategy good-good of game theory, i.e. the tactics of constant compromises, is often more unsuccessful than the strategy of loss-loss. The second one talks about a smaller minus for the sake of a bigger plus, about stumbling, swinging, or chess-wise about a gambit. Strategy is an art of sacrifice. Nature can be our best teacher, it is written in the mentioned article. Successful adaptation through favorable variations of organisms reveals seemingly unfavorable advantages.

In this battle for survival, the common red clover devised an extraordinary strategy. Its flower has a unique feature — a long, thin funnel that leads to nectar at the base. Only bees that have very long tongues can get sweet nectar. Other insects are excluded. It is a strategy based on what this plant "decided" not to do.

The beauty of this choice is that the bees fly away from other insects, stopping at more flowers and thus increasing the chances of successful pollination. In fact, red clover has created an exclusive alliance with bees that ensures that its pollen is distributed more widely than other plants, giving it a key competitive advantage. Of course, it is not without risk, because what if another plant produces nectar with a sweeter taste and the bees "replace the brand", or what if the bees become extinct? However, red clover gambit has a significant advantage that no other plant has been able to usurp.

The following example is an article about Hard work that often does not pay off. Almost half of the people in the EU work in their free time to meet the demands of the job, and a third often or always work at high speed, according to the latest estimates, but with so much effort there is no adequate income.

The idea of success through risk is natural to information theory (Еxtremes), and shortly before that it was confirmed in game theory. These two agree on the usefulness of tactical "retaliation", i.e. the "Tit-for-tat" strategy, which is approximately our "eye for an eye and kind for dear". Let me remind you, these theories often start from coincidence and are confirmed statistically when we cannot expect good results from them without exception.

Capablanca

Question: Why do you think conscientious work is not enough for greater success?

Answer: Good question, I understood even though it sounds silly at first. I believe it is related to the previous attachment (Success), so I will answer that way. There is a further explanation of the above "explanation".

By working properly, we adhere to the rules that is the restrictions, which further means that we are lagging behind. The tissue of action is information, and its deepest essence is uncertainty, not predictability. Doing by the guidelines, we do not go beyond our range of predictability, while conditions can change imperceptibly for us, and our rules can lag behind. In time, when the well-established and elaborate "perfection" is found in a "hostile" environment, we realize that we have "rusted".

In the top game, we find confirmation of this "theory" more often (easier) than in the average, precisely because of its once tidiness. All civilizations therefore have their own lifespan, because if they are more successful, they will stick to proven routines and feel worse on the "slippery" terrain of other options. That is why genetic mutations are not only a weakness but also a blessing of life on earth.

Question: What would be an example in playing chess?

Answer: The example of Cuban José Raúl Capablanca (1888–1942) and his match (1927) for the defense of the world title against the Russian grandmaster Alexander Alekhine (1892-1946) could be cited in chess. Capablanca was and remains a phenomenon in that during the ten years of his rule as the world champion in that game, he lost only one single game — from the hitherto unknown Réti (1924).

Anyone who follows chess knows that it is almost impossible for even the best not to lose a game, even during just one match, and Capablanca has not lost them in a series of ten years! At the same time, he played against the best in the world (world champions rarely go to weak tournaments). He was defeated firstly because his technique, style, knowledge of position, attack and defense in that game were perfect. But also, because he came across Richard Réti (1889–1929), a Czechoslovak grandmaster who "went wild" from the first move. Reti game, one of the strangest chess openings, is still played today when we want to confuse the opponent, get him off track.

Something similar happened to Capablanca in the defense of the title of World Chess Champion against Alekhine. This challenger liked to create strange positions (for the actual champion), to play "against the rules", to take too tasteless risks, but to master his "murky" waters with great skill. Capablanca lost his match and with it the title, desperately defending from defeat, to the astonishment of the entire chess world, including Alekhine himself.

Question: Could this also be a weakness of von Neumann's strategy?

Answer: Yes, that could be the weakness of the strategy of the Hungarian-American mathematician John von Neumann (1903–1957). His Minimax theorem (1928), in open game where the best move leaves the opponent the worst opportunity, has limit in predictability. When the boundaries are visible, recognizable, the game is too simple, boring and not grandmaster, but when they are inconceivable, then the above applies to it.

Overstated

Question: How to save the birth rate?

Answer: To stop "legalization" in the sense of "children are a danger" for existence, career, but also present in opportunities to punish parents by the state for violating "children's rights" and other generally accepted goals of society. On the survival is already being done with the help of (small) financial support to mothers, but that will not be enough if mothers and families are not given a career perspective in which children are not a hindrance. Society asks women to think about their own careers and they respond to those "calls". In addition, state power and "children's rights" are a growing threat to parenthood, where the fear of punishment narrows the space for idyllic "offspring".

Read my repeated answer to similar questions about Natality. Modern civilization is making more and more progress in enslaving the working people. What were once priorities, reserved for slaves, serfs, servants, in terms of vassal labor or wages, is perfected today. The system of employment and business relations, financial obligations and deprivation of our free time, includes an increasing percentage of the population, and at the individual level it is becoming more austere.

By reducing freedoms, we thus evolve into individuals, cells of the state tissue, which are more specialized but more and more similar, gradually duller and less reproductive. We will often see comparisons with companies and corporations in explanations of the tissues of a living organism in popular science explanations, and it is true that modern society, by focusing on better organized legal and economic systems, becomes like a biological living organism. It is a form that nature will repeat, imitate like a quadratic equation whose applications we find in "completely unconnected" places, that is, ways.

Unlike the production of inanimate matter in crafts and factories largely mastered, the reproduction of a living being defies the principled minimalism of information. Life is a rarity, given the size of the universe. Its "leaks" through the paradoxes of principled minimalism, otherwise less often than in the case of storms, volcanoes and geysers — which also oppose minimalism (action). By arranging things we organize them, so we mostly reduce their "scattering" and our own information. But, like the storm, which we will rather restrain than wave by randomly adding restrictions to it, today's Western way of life, not completely knowing the reasons, suffocates the birth rate.

With growing legal restrictions on the birth rate and its abandonment to the natural flows of critical culture, whether consciously or not, it restrains population growth. Excess information is a characteristic of life. But for information, the law of conservation applies, which parents must share with work and financial obligations, with fears of the state laws and other reductions of options offered to potential parents by a "virtuous new world", and the mentioned organization that prevents waving happens.

Religion

Question: Is there a god?

Answer: It is logical for me to get such difficult questions, and then it is logical to try to answer to such. But I'm sorry, I'm failing. Let's be realistic, the greatest minds have been breaking spears for millennia about the existence of a god or at least about the question of what such a being could represent. Without success, in my opinion.

The British mathematician Bertrand Russell (1872-1970) was withal a philosopher and a lawyer (he was the founder of Russell's court for condemning American crimes in Vietnam and around the world), and he won the Nobel Prize for Literature in 1950. Russell was a great opponent of religion, and especially ridiculed the Catholic Church, the papal mendacity and considered unforgivable the crimes of the past of their institutions.

Russell drew the philosophical basis of his anti-religious beliefs from the so-called Russell's paradox, according to which there is no set of all sets, that is, such a complete and closed whole, no matter what it consists of, which encompasses everything and is self-sufficient. Kurt Gödel (1906-1978) followed the path of Russell's thinking and managed to prove that mathematics cannot prove itself. At the same time, he proved that there is no (mathematical) knowledge that could contain all the knowledge, not even what might once have been mathematical.

From the standpoint of "information theory" (mine, not yet recognized), I could say that Russell and Gödel talked about the same thing, that this world consists of information whose ultimate essence is uncertainty. In that sense, the whole cosmos, no matter how great it is considered, is always an unfinished topic. But then the existence of God, more precisely the question of religion, is reopened.

It is not possible to accept mathematics as a truth that would encompass everything, nor is it possible to dispute anything as we know it today, and on the other hand, things are somehow the same with religion. Religion and mathematics, spirituality and rational, whether they could be two friends or opponents, take whatever you want, for now they have no way to meet, get to know each other, make friends or go to war (in a figurative sense, I suppose), whatever. But such a dilemma is no longer enough for us, because my theory of information of similar (un) friends predicts more.