Problems involving circles are among the most interesting in the mathematics. To learn these problems one should solve it independentlu, not looking even at the given solutins.
Definitions
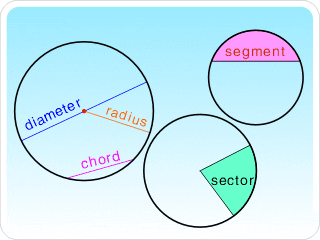
Circle is the set of points in plane on the same distance from the fixed point. The fixed point is named centre, and the fixed distance is radius.
Chord is the line joining two points on a circle. When the line passes through the centre, the chord is diameter.
Tangent is a straight line which touches a curve at a point. A tangent to a circle is at right angles to the radius of the circle at its contact.
When a straight line is drawn joining two points on the circumference of a circle it divides it into two parts, the minor segment and the major segment.
The region of a circle formed by two radii and part of the circle's circumference is called a sector of the circle.
The smaller region formed is called the minor sector, the larger region formed is called the major sector.
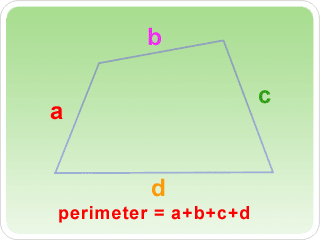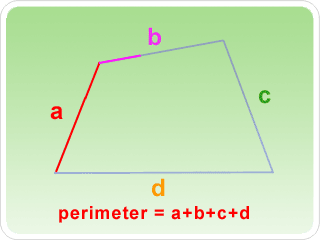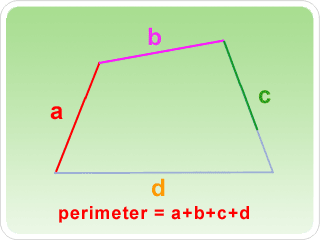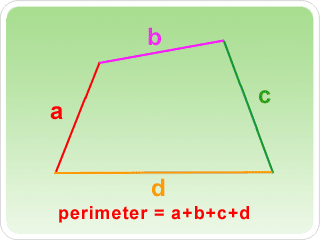
Perimeter of the shape is the name given to the boundary of the shape. It is also sometimes used to mean the length of the boundary.
 |
 |
Inscribe means to draw inside. When one shape fits inside another it is said to be inscribed. For example, a circle can be inscribed in a triangle to touch the sides, and a square can be inscribed in a circle so that its vertices (a plural of vertex) are on the circle. The vertex is the intersection of two sides of a plane figure.
Semi means 'half'. A semi-circle is half of a circle formed by cutting along a diameter.
Assertions
A tangent to a circle is at right angle to the radius of the circle at its contact.
If A, B and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle.
Problems
1. Let k be an outside inscribed circle that connects the side BC and extensions of BA and CA of the triangle ABC. Prove that tangent from vertex A to the connect point of k is equal to semiperimeter of the triangle.
Solution
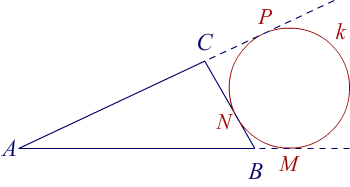
On the graph above are tangents long from A to circle k in points M and N. Tangent lines AM and AN are equal. Also, BM = BN and CP = CN.
Hence, perimeter of the circle is AB + BC + CA = AB + (BM + CP) + AC = (AB + BM) + (CP + AC) = 2×AM, ie. semi perimeter = AM.♦
2. Let s be a semi perimeter and c hypotenuses of given rectangular triangle, than the radius of the inscribed circle is s – c.
Solution
Projections of the center of (inscribed) circle to sides a, b and c are successively M, N and P (draw!). That are points on sides BC, CA and AB of the given rectangular triangle, with right angle at the point C, and semi radius of the circle r = CM = CN. Tangent lines, drown from points of the triangle to the inscribed circle are equal. So the perimeter of the triangle is 2s = AB + BC + CA = 2AP + 2BP +2r = 2c + 2r. Hence s = c + r, i.e. r = c – r.♦
3. Circles k1 and k2 have contact in point A. Chord a, containing point A, cuts these circles respectively at points P1 and P2. Prove that tangents of given circles in points P1 and P2 are parallel.
Solution
Triangle P1AO1 is isosceles, as triangle P2AO2 too. Consequently, all four angles AP1, P1AO1 ..., are equal, so the angles between tangents and given chords are equal. Meaning, the tangents are parallel.♦
4. Circles k1 and k2 have contact outside in point A. Their common tangent connect the circle k1 in point B, the circle k2 in point C. Prove, the angle BAC is rectangular.
Solution
Let t1 and t2 be common tangents of given circles (draw!). Intersection of the tangents is point S. From SA = SB = SC follows that S is center of the circle passing by points A, B, C, whereas the BC is diameter. Meaning, the angle BAC is rectangular.♦
5. Given are the circle k(O, r) and its tangent a with connection point A. The tangent a has points B and C with tangents line BD and CE ending on the circle k. Prove that angles BOC and DAE are equal or supplementary (whose sum is 180°).
Solution

Chord AD is perpendicular to line OB (of radius) in point F, graph above. Rectangular triangles BOA and BAF have common angle in point B, so they have all tree corresponding angles the same. Thus, angle BOA is complementary (the sum of the measures of two angles is 90°) with angle DAO, so BOC and DAE are supplementary angles.
6. Let AP and AQ be tangent lines on the circle k(O, r). If through any point M of the circle in major segment PQ a tangent that passes lines AP and AQ successively in points B and C, prove that AB + AC – BC and angle BOC are constant.
Solution
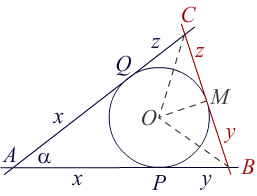
First, AB + AC – BC = (x + y) + (x + z) - (y + z) = 2x = const. Second, ∠CBA + ∠ACB = 180° - α and ∠MOB + ∠CBA/2 = 90°. Thus ∠BOM = 90° - ∠CBA/2, ∠MOC = 90° - ∠ACB/2, so ∠BOC = ∠BOM + ∠MOC = (90° - ∠CBA/2) + (90° - ∠ACB/2) = 180° - (∠CBA + ∠ACB)/2 = 180° - (90° - α/2) = 90° + α/2 = const. for given α = ∠BAC.♦
7. Given are circle k, its diameter AB and point P near circle beside line AB. Using only ruler, construct perpendicular line through P to line AB.
Solution
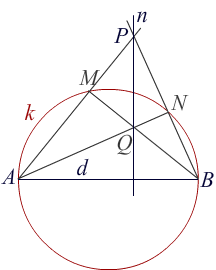
If the point P is outside the circle, lines AP and BP intersects the circle in points M and N. Then AN⊥BP and BM⊥AP. Let the intersection of lines AN and BM be point Q. Line PQ is required normal (line n on drawing above), the third height of a triangle ABP. If the point P is inside circle, points P and Q change its roles.♦
8. Given angle 19° divide to 19 equal parts using only pair of compasses.
Solution
Draw by compasses a circle with center in top of the given angle. Increase, transfer given angle 19 times. Forasmuch as 19×19 = 361 we have central angle 1°. Adding obtained angle into given angle, we have requested parts.♦
References
Translated from Serbian: Krugovi